 |
NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Leyes de Newton, dinámica del movimiento circular, péndulo cónico)
|
|

|
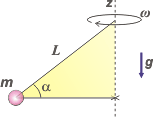
NMS d3.15*- (Péndulo cónico) Un cuerpo de masa m = 600 g gira alrededor de un eje vertical z convelocidad angular constante ω = 5 s -1, como muestra la figura. Describe una trayectoria circular paralela al piso. La soga de longitud L = 1 m es inextensible y de masa despreciable.
a) Calcule el módulo de la tensión de la soga.
b) Calcule la velocidad tangencial, vt, de la masa. |
 |
|
Un ejercicio más de péndulo cónico, pero con algunas diferencias interesantes. Como siempre, hay que arrancar con un DCL, pero también voy a hacer un esquemita del péndulo (ahora en perspectiva) que creo que te va a ayudar y seguro que lo usaremos durante la resolución del ejercicio. |
|
|
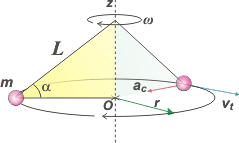 |
Cosas destacables del esquema. La circunferencia que describe el péndulo es horizontal y tiene su centro en O (¡no en el techo!), y su radio r. En una posición -de cuando viaja por atrás- aproveché y te dibujé un vector aceleración centrípeta, ac , y una velocidad tangencial, vt , ¿te cierra todo? |
|
|
|
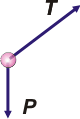
Bueno, acá está el DCL, mostrando las dos únicas fuerzas que actúan sobre el péndulo cuando se halla en la misma posición que te lo dibujé en el esquemita. La fuerzas son: el peso de la masa, P; y la tensión con que lo tira la cuerda, T. |
|
|
 |
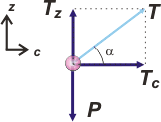 |
Bueno, tenemos que escribir las ecuaciones de Newton, pero, como las fuerzas no son co-direccionales, debemos descomponer una de ellas. Lo más práctico es descomponer T. A la derecha va de nuevo el DCL, pero con la T descompuesta.
Recordás que siempre que enfrentás un MCU a uno de los ejes lo llamás c (por centrípeto), en lugar de x, ¿no? Es cierto que se trata de un eje que va cambiando con el tiempo. Pero no te olvides que la dinámica son sólo instantáneas del universo. |
|
|
|
Fijate que α es el ángulo del hilo con la horizontal (no con la vertical como es costumbre), eso permite establecer que:
Tz = T . sen α
Tc = T . cos α
Ahora sí, vamos a Newton. En el eje vertical tenemos que la aceleración es cero (la circunferencia no cambia de altura). |
|
|
| |
ΣFz = 0 |
→ |
Tz — P = 0 |
→ |
T . sen α = m . g |
[1] |
|
| |
ΣFc = m ac |
→ |
Tc = m ac |
→ |
T . cos α = m ω² . r |
[2] |
|
|
|
|
Como el enunciado habla de la velocidad angular y del radio, elegí reemplazar la aceleración centrípeta por aquella expresión que contiene ω y r. En la ecuación [2] tenemos casi todo, sólo nos falta reemplazar el radio de giro, r, por su elquivalente en función de la longitud del hilo, L, y el ángulo α. Mirá el triangulito amarillo del esquema:
r = L . cos α
Metemos eso en la ecuación [2]...
T . cos α = m ω² . L . cos α
El coseno del ángulo -valga lo que valga- se cancela.
T = m . ω² . L
T = 0,6 kg . 25 s -2. 1 m
|
|
 |
|
|
|
Para conocer la velocidad tangencial vamos a necesitar conocer α. Para eso usamos la ecuación [1].
T . sen α = m . g
de donde:
sen α = m . g / T
sen α = 0,6 kg . 10 m/s² / 15 N
sen α = 0,4
α = 23,58°
Con ese dato nos vamos a la relación fundamental de la velocidad angular y tangencial:
vt = ω . r
vt = ω . L . cos α
vt = 5 s -1 . 1 m . cos 23,58°
|
|
|
|
|
|
| Y nos sacamos un 10. No es habitual que un ejercicio de péndulo cónico tenga por incógnita el ángulo de apartamiento del hilo con la vertical, y menos aún que en lugar de referirnos a ese ángulo lo hagamos a su complementario. Pero vos ya sabés cómo son los físicos... tienen una enorme y maligna imaginación. |
|
 |
| *Este ejercicio formó parte del segundo examen parcial tomado en nov-13. |
|
|
| DESAFIO: ¿Cuál es la relación entre la aceleración de la gravedad y la aceleración centrípeta? |
|
| Algunos derechos, zurdos y ambidiestros reservados.
Se permite su reproducción citando la fuente. De los ambidiestros también. Última actualización nov-13. Buenos Aires, Argentina. |
|
|
|

