home  | más de dinámica | otros temas de Física | lecciones del maestro Ciruela | tonterías |  @ 
NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
  

¡no me salen!

NMS 3.12- Una piedra de 3 kg atada a una soga horizontal describe una trayectoria circular de 2 m de radio sobre una mesa horizontal que se encuentra a 1,25 m del suelo. Va aumentando cada vez más la velocidad hasta que la soga se rompe. Si ésta resiste un esfuerzo máximo de 54 N hasta cortarse, la distancia horizontal desde donde abandona la mesa hasta la zona de impacto de la piedra contra el piso es, aproximadamente:

       a) 6 m       b) 6 m       c) 10 m        d) 5 m       e) 3 m
       f) ninguna de las respuestas anteriores

Como en tantos otros casos tenemos un ejercicio que combina habilidades de dinámica y cinemática. Una parte del enunciado describe un movimiento circular cuyo planteo nos va a permitir saber con qué velocidad sale despedida la piedra de la mesa. Y en la segunda parte, claramente cinemática, averiguaremos la distancia al pie de la mesa en que impacta sobre el piso.

    

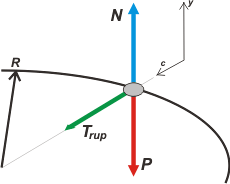Tal vez te haga un poco de ruido el hecho de que la velocidad angular de la piedra vaya en aumento. Eso no tiene que hacerte problema: no te olvides que la dinámica representa una foto, una instantánea de universo. Lo que a nosotros debe interesarnos es justamente ese instante en el que la cuerda se rompe. En ese instante la tensión de la cuerda alcanza su valor de ruptura, Trup, y desde ese instante comienza otro movimiento.
 

Esa es la foto representada por nuestro esquema: un móvil que mueve sobre una trayectoria circular justo en el momento en que se corta la soga.

Trup = m . ac

Trup = m . v² / R

De ahí depejamos la velocidad en la que la cuerda se rompe:

v² = Trup R / m

v² = 54 N . 2 m / 3 kg

v² = 36 m²/s²

v = 6 m/s

Ya tenemos la velocidad con la que el cuerpo sale despedido de la mesa. Vamos a la cinemática:

  

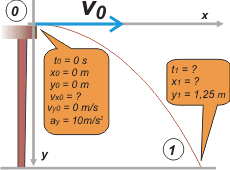
Infaltable nuestro esquema. Llamé 0 a la salida desde la mesa y 1 a la llegada al piso. Se trata, obviamente de un TO; más precisamente un tiro horizontal (ya que supondremos que esa mesa es horizontal) de modo que la velocidad vertical en 0 es nula. Las ecuaciones nos quedan así:

x = 6 m/s . t

y = 5 m/s² . t²

 

A esas dos ecuaciones les pedimos que hablen de la llegada al piso:

x1 = 6 m/s . t1

1,25 m = 5 m/s² . t1²

De la segunda surge que t1 es igual a 0,5 s. Y si metemos eso en la primera obtenemos la respuesta al ejercicio.

  
  x1 = 3 m respuesta e)
 

Desafío: ¿Cuá sería la tensión de ruptura si la piedra alcanzaba el piso a 6 metros?

 
 
Algunos derechos reservados. Este material didáctico no puede ser comercializado... Pero podés leerlo, memorizarlo, olvidarlo, imprimirlo, copiarlo, prestarlo, compartirlo, regalarlo, atesorarlo, y muchas cosas más. Última actualización jun-12. Buenos Aires, Argentina.