 |
NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Leyes de Newton, dinámica del movimiento circular)
|
|

|
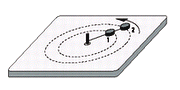
| NMS d3.06- El sistema de dos cuerpos de la figura gira
en una mesa horizontal con rozamiento despreciable,
de modo que los cuerpos se hallan alineados
con el centro y realizan 2 vueltas por segundo.
Si las masas respectivas son: m1 = 0,5 kg;
m2= 1,5 kg, determinar las intensidades de las
fuerzas sobre cada cuerda. Cada tramo tiene
0,5 m de longitud. |
 |
|
| Pero qué problema más bonito... no se imaginan cómo lo amo debido a las visicitudes que me trajo en la vida. Empecemos, claro está, con los DCL. |
|
|
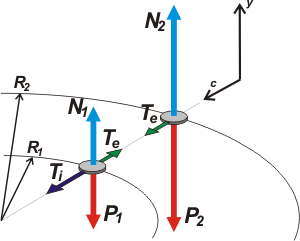 |
Como hay dos sogas diferentes, una la que une el clavo con el cuerpo 1 y la otra la que une el cuerpo 1 con el 2, le puse a las tensiones nombres diferentes: Ti (tensión interna) a la primera, y Te (tensión externa) a la segunda, que, como toda cuerda del CBC realiza iguales fuerzas en ambos extremos, uno sobre el cuerpo 1 tirando hacia afuera y otro sobre el cuerpo 2 tirando hacia adentro. |
|
|
|
Ya podemos pasar a las ecuaciones de Newton. En este problema las ecuaciones en el eje vertical no van a aportar información interesante. Igual las escribo.
Cuerpo 1 → ΣFy = m1 a → N1 — P1 = 0
Cuerpo 2 → ΣFy = m2 a → N2 — P2 = 0
Las ecuaciones del eje que tiene la dirección radial, en cambio, nos van a resolver el problema:
Cuerpo 1 → ΣFc = m1 ac1 → Ti — Te = m1 ac1
Cuerpo 2 → ΣFc = m2 ac2 → Te = m2 ac2
fijate que le puse un subíndice particular a la aceleración de cada cuerpo... ¡es que son diferentes! ac1 ≠ ac2. Estamos acostumbrados a que la aceleración del "sistema" sea una sola y la misma para todos los cuerpos. Pero acá son diferentes, ya que la velocidad angular (y la frecuencia) es la misma para ambos, pero los radios son diferentes, R1 = 0,5 m y R2 = 1,0 m. Por un lado tenemos que:
ω = 2π . ƒ
ω² = 4π² . ƒ²
Y siendo que ac = ω² . R
ac1 = 4π² . ƒ² R1 = 4π² . 4 s-2. 0,5 m = 79 m/s²
ac2 = 4π² . ƒ² R2 = 4π² . 4 s-2 . 1 m = 158 m/s²
Haciendo números...
Te = m2 ac2 = 1,5 kg . 160 m/s²
|
|
|
|
|
|
Ti = m1 ac1 + Te
Ti = 0,5 kg 79 m/s² + 237 N
|
|
|
|
|
|
| |
|
|
DISCUSION: Seguramente ya te dijeron (y si todavía no te lo dijeron, ya te lo van a decir) que las fuerzas centrífugas no existen. Es mentira. Mirá, acá te cuento la historia del día que me echaron de la sociedad de físicos y desde entonces doy clases a escondidas. La cuestión es que no existen -per se- ni las fuerzas centrífugas ni las centrípetas. Ser o no ser centrífugo, o centrípeto, es simplemente una característica geométrica, consistente es estar permanentemente apuntando hacia un centro o desde un centro. Del mismo modo en que tampoco existe -por naturaleza propia- la fuerza normal. Ser normal sólo significa que forma 90 grados con alguna superficie.
Mirá el cuerpo 1 de este problema, por ejemplo. La fuerza Ti apunta permanentemente hacia el centro de giro, luego es centrípeta. Y la fuerza Te apunta permanentemente hacia afuera del círculo, y con dirección radial... es inequívocamente centrífuga.
Lo que afirma Newton (aquí está el error de estos chabones que me echaron) es que la resultante (la sumatoria de todas las fuerzas que actúan sobre un cuerpo animado de MCU) es centrípeta. Pero nada dice sobre todas y cada una de las fuerzas que componen esa resultante. |
|
 |
| DESAFIO: En este problema hay una fuerza centrífuga más... ¿cuál es? |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Agradezco las atentas lecturas de Andrés Montero y Matías Santoro que detectaron sendas erratas y enviaron gentilmente la correción. Última actualización oct-06. Buenos Aires, Argentina. |
|
|
|

