NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Leyes de Newton, dinámica del movimiento circular, péndulo cónico)
|
|

|
NMS d3.04- Un pescador revolea una plomada de
200 g, atada al extremo de una línea, de modo
que gira en una circunferencia horizontal de 1 m de radio, y realiza 2 vueltas por segundo. Hallar
con qué velocidad partirá la plomada, cuando
suelte la línea. ¿Qué fuerza horizontal se requiere
para mantener girando la plomada? Analizar si
el hilo puede permanecer horizontal, y si la intensidad
de la fuerza que ejerce es o no igual a la
calculada.
|
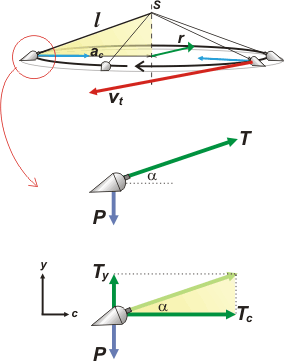
El pescador sostiene la tanza de la plomada en el punto S (por suspensión). Como ves el piolín de largo l, queda un poco oblicuo (después volvemos sobre ese tema, ¿ok?) y al girar genera un cono (jerga). ¿Vamos bien?
La base del cono está horizontal, ese dato lo da el enunciado. La plomada describe una circunferencia de radio r (está marcado en verde). Si el pescador la suelta sale despedida con la velocidad, vt, que tenga en ese instante (marcada en rojo). |
|
|
 |
Dada la velocidad angular, se puede calcular la tangencial:
vt = ω . R =
vt = 2 . 2πs-1. 1 m = |
|
Tomé una instantánea justo cuando la plomada pasaba por el extremo izquierdo. Y te la amplié abajo. Fijate, que la aceleración centrípeta apunta hacia el centro (flecha celeste) de la circunferencia, y no hacia la mano del pescador.
Las fuerzas que actúan sobre la plomada son dos: su propio peso, P, y la tensión que hace la tanza, T.
Como no son colineales, descompuse T en dos direcciones |
|
|
|
Una de ellas TC , es la fuerza horizontal por la que pregunta el enunciado.
ΣFC = m aC
TC = m ω² . R
TC = 0,2 kg 16 π² . s-2. 1 m
|
|
|
|
| La componente vertical equilibra al peso. Si esa componente no existiese la plomada estaría animada con una aceleración vertical. De modo que para evitar eso Ty no puede valer cero. De modo que la tensión que hace el hilo, y que necesariamente tiene la misma dirección que el hilo, no puede ser horizontal nunca. |
|
|
|
|
| DISCUSION: Sin embargo todos nosotros vimos que los pescadores revolean sus plomadas con mucha velocidad y logran que la tanza quede horizontal... ¡Hay mi pequeño imberbe (y si eres pequeña, con más razón eres imberbe)! cuanto mayor sea la velocidad mayor será la fuerza centrípeta y menor el ángulo de inclinación, hasta el punto de que no podamos detectarlo. Ni hablar de las inevitables (o hechas adrede) aceleraciones verticales que pueden enmascarar el fenómeno que acabamos de describir. ¡Qué plomada! |
|
 |
| DESAFIO: Supongamos que la circunferencia es oblicua, o vertical... ¿qué cosas cambian en esa situación respecto de este ejercicio ? |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Nobody told me nada. Última actualización dic-06. Buenos Aires, Argentina. |
|
|
|

