NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Leyes de Newton, dinámica del movimiento circular)
|
|

|
 |
NMS 3.02 - El tambor de un lavarropas tiene 60 cm de diámetro, y gira a 600 rpm alrededor de un eje
vertical. Calcular la intensidad de la fuerza horizontal
que sus paredes hacen sobre el botón
suelto de una camisa, cuya masa es 5 g. Comparar
con el peso del botón. |
|
| Adivina adivinador ¿por dónde se empieza mejor? Por un DCL, ofcors. |
|
|
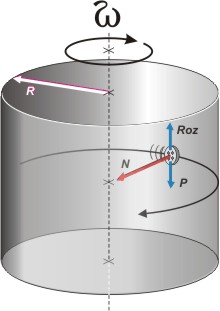 |
Bueno, yo encuentro (y mirá que tengo experiencia) tres fuerzas. El peso, P; lógicamente, no te la tengo que explicar. Algún rozamiento tiene que haber con la pared y debe apuntar hacia arriba ya que no hay ninguna otra fuerza que apunte para arriba, y si no la hubiese el botón no podría quedarse siempre a la misma altura, se iría para abajo tironeada por su peso. (Ya volveré sobre el tema en la discusión). De modo que: Roz.
Por último la fuerza principal (y ya verás que la mayor) de todas las fuerzas en este problema que es el apoyo en la pared interna del lavarropa, que obviamente es perpendicular -o normal- a la superficie, N.
Vos creeme; y si no, no importa. |
|
|
|
| Ok, vamos a las ecuaciones: |
|
|
ΣFy = m ay → Roz — P = 0
ΣFc = m ac → N = m ac
en lugar de escribir ac buscaremos su equivalente que más se aproxime a los datos aportados por el problema, en este caso ac = ω² . R. Como tenemos todo lo que hace falta ya podemos calcular la fuerza de contacto. Pero antes de entrarle a esta ecuación, tenemos que pasar las magnitudes a unidades del sistema internacional (¿viste?) empecemos por la velocidad angular:
ω = 600 rpm
ω = 600 2π / 60 s
ω = 62,83 s-1
Ahora sí. Vamos:
ω² = 3.950 s-2
R = 0,3 m
ac = 1.185 m/s²
m = 0,005 kg
Entonces:
N = 0,005 kg . 1.185 m/s²
|
|
|
|
|
|
Si la queremos comparar con el peso debemos conocer primero el peso. P = m . g
P = 0,05 N
|
|
|
|
|
|
| |
|
|
| DISCUSION: La fuerza que hace el tambor es 120 veces mayor que el peso. Fijate hace falta apenas un coeficiente de rozamiento de 0,01 (o sea una nada), para compensar el peso. Siempre, sea lo que sea, se va a quedar pegado contra la pared. Las rotaciones generan aceleraciones muy altas, que a su vez generan fuerzas muy altas. Es el método más práctico para generar fuerzas enormes y capaces de, por ejemplo, separar partículas pequeñas. En un laboratorio cualquiera de bioquímica existen centrífugas que pueden generar aceleraciones centrípetas de 100.000 g, o sea 1.000.000 m/s². Claro, deben funcionar refrigeradas y en vacío, si no, las altas fricciones con el aire la recalentarían. |
|
 |
| DESAFIO: Hallar la velocidad angular para una ultracentrífuga de 100.000 g con 25 cm de radio y la fuerza ejercida sobre una partícula viral de 1 pg. |
|
| Se permiten todos los derechos reservados.
Se reserva su reproducción fuenteando la cita. Última actualización oct-06. Buenos Aires, Argentina. (Algo anda mal en este mensaje). |
|
|
|

