NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Leyes de Newton)
|
|

|
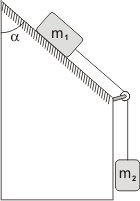
NMS d2.19* - Dos masas inicialmente en reposo se encuentran unidas por una soga inextensible y de masa despreciable como muestra la figura. Considere que entre m1 y el plano inclinado hay rozamiento.
a) Graficar el diagrama de la partícula libre para las masas m1 y m2.
b) Si el coeficiente de rozamiento estático es μe = 0,7 y α = 60º. ¿Cuál es la máxima m2 para que el sistema esté en equilibrio? Suponga que m1 es un dato. |
 |
|
| |
Ejercicio sencillo si los hay. Aunque tiene algunas "rarezas" que a los desprevenidos le pueden costar el punto. Vamos a resolverlo, y te voy a ir contando cuáles fueron los errores más comunes de los estudiantes en sus intentos de resolución. |
|
|
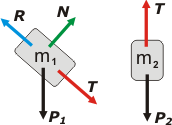 |
Como todo ejercicio de dinámica, hay que comenzar por los diagramas de cuerpo libre, DCL.
Las fuerzas que actúan sobre el cuerpo 1 son: su propio peso, P1; su apoyo sobre el plano, N; la fuerza con que lo tira la soga, T; y el rozamiento con el plano, R. Son 4 fuerzas, ni una más ni una menos. |
|
|
|
Las fuerzas que actúan sobre el cuerpo 2 son solamente su propio peso, P2, y la fuerza con que lo tira la soga, T. Los sentidos de las fuerzas están dados por las flechas, los largos, en cambio, que indican el módulo, son arbitrarios.
Como las fuerzas que intervienen en el cuerpo 1 no son codireccionales, vamos a tener que elegir un sistema de referencias, SR, y expresar las fuerzas (descomponiendo las necesarias) en sus direcciones. El adecuado es el que elijo acá abajo, que sólo requiere descomponer P1. |
|
|
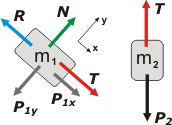 |
El SR hay que dejarlo indicado. Cualquiera de estos dos pares de DCL se da por bueno, y son utilísimos para seguir resolviendo el ejercicio.
En éste, como en cualquier ejercicio de dinámica, después de concluir los DCL se procede a escibir las ecuaciones de Newton, en nuestro caso tres: dos para el cuerpo 1 y una para el cuerpo 2. |
|
|
|
| |
Cuerpo 1, eje x |
T + P1X — R = 0 |
[1] |
| |
Cuerpo 1, eje y |
N — P1y = 0 |
[2] |
| |
Cuerpo 2, eje x |
P2 — T = 0 |
[3] |
| |
Rozamiento |
R = μe N |
[4] |
|
|
|
Te cuento algunas peculiaridades de este sistema de ecuaciones. Primero, fijate que puse aceleración igual a cero, a = 0, en todas direcciones. En efecto, eje enunciado del ejercicio dice "¿Cuál es la máxima m2 para que el sistema esté en equilibrio?". Que el sistema esté en equilibrio significa justamente eso: aceleración nula.
Otra cuestión: el valor máximo que puede tener el cuerpo 2 sin que se rompa el equilibrio se corresponde, justamente, con el valor máximo que puede soportar el rozamiento que no es otro que el rozamiento estático máximo, R = μe N. |
|
|
Todavía falta otra peculiaridad, que viene ahora. No sabemos quiénes son P1X ni P1y. pero tampoco hemos utilizado el valor de α, y es claro que con su ayuda lo vamos a lograr. Pero ojo: en este ejercicio α es el ángulo que el plano inclinado forma con la vertical, cuando 99 de cada 100 ejercicios de plano inclinado nos ofrece el ángulo que se forma con la horizontal. ¡Maldita trampa!
Ahora, que si recurrimos a un esquemita auxiliar para buscar un triángulo rectángulo adecuado... podemos sortear la trampa sin ningún rasguño.
El ángulo α (la inclinación del cuerpo 1) vuelve a aparecer a la derecha de P1, por lo tanto, si mirás el triangulito rectángulo que te sombré en amarillo... resulta que:
P1X = P1 cos α
P1y = P1 sen α
|
|
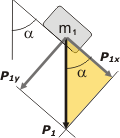
Los ángulos α son correspondientes entre paralelas. El triángulo es rectángulo (requisito de la descomposición vectorial). P1X es adyacente a α. Más no puedo hacer. |
|
|
|
Ahora sí, combinando las cuatro ecuaciones (el orden en el que lo voy a hacer acá es irrelevante, vos deberías probar el tuyo) aparece una expresión que vincula m1 con m2, y eso es justamente lo que pide el enunciado.
Meto la [3] y la [4] en la [1]:
P2 + P1X — μe N = 0
Meto la [2] en ésta:
P2 + P1X — μe P1y= 0
Reemplazo las componentes de P1 por sus iguales.
P2 + P1 cos α — μe P1 sen α = 0
m2 g = — m1 g cos α + μe m1 g sen α
m2 g = m1 g (— cos α + μe sen α )
m2 = m1 (— 0,5 + 0,7 . 0,866 )
|
|
|
|
|
|
| Tampoco es habitual que en un examen pidan un valor expresado no numéricamente sino en función de otra magnitud no numérica. Pese a que No me salen trabaja mucho con este tipo de relaciones que son mucho más ricas que los resultados numéricos, los estudiantes prefieren "contar con los dedos". |
|
|
| |
|
|
DISCUSION: La única vacuna contra las rarezas son "horas de vuelo", experiencia, resolver muchos ejercicios, comprar una suscripción anual a No me salen (es gratis, no llores). |
|
|
| *Este ejercicio pertenecía al tema de examen parcial de Física tomado el 1 de octubre de 2010 en diversas sedes del CBC. |
|
|
|
| DESAFIO: ¿Cuánto valdría el rozamiento estático si el conjunto quedase en reposo y si m2 = 0,1 kg y m1 = 3 kg ? |
|
 |
| Algunos derechos reservados.
Se permite su reproducción bajo la solemne promesa de citar la fuente. Última actualización oct-10. Buenos Aires, Argentina. |
|
|
|

