home  | más de dinámica | otros temas de Física | lecciones del maestro Ciruela | tonterías |  @ 
NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Leyes de Newton)

  

¡no me salen!

NMS d2.18 -Un bloque de 6 kg descansa, como se indica en la figura, sobre la pieza en forma de L de 10 kg. Los coeficientes de rozamiento entre ambos son µe = 0,30 y µd = 0,25, y no hay rozamiento en la polea (sin masa) ni el plano horizontal con la pieza en L. Determinar:
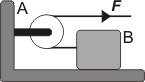Determinar: la fuerza máxima que se puede ejercer en la cuerda para que el bloque B no deslice sobre A y la aceleración en dicho caso.
 

Bien... esto es terrible. Pero igualmente vamos a empezar por los correspondientes DCL. Como tenemos dos cuerpos, trendremos dos DCLs.

Notarás que los deformé un poquito... son licencias que uno se toma en la vida y que le dictan los instintos didácticos. La pieza en "L" la soldé con la polea para hacerla un cuerpo único, la engordé un poquito y no te quepa duda que a los efectos de este ejercicio es lo mismo, sólo que a mi instinto le me parece un poco más claro.

    
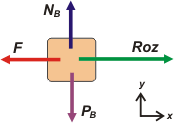Empecemos por el cuerpo B que es más sencillo. Lógicamente sobre él actúa la Tierra atrayéndolo hacia abajo, PB. El cuerpo A le hace una fuerza hacia arriba para sostenerlo, NB. La soga tira del cuerpo hacia la izquierda con esa fuerza máxima que nos pide hallar el enunciado, y que llamaré sencillamente F. Pero A y B se hallan trabados por el rozamiento, que pediremos que sea el rozamiento máximo estático que pueda establecerse entre ambas superficies, y que yo voy a llamar Roz.
Cuando hacés el DCL lo importante es que aciertes las fuerzas que actúan, su dirección y sentido. El módulo vendrá con las ecuaciones, y no debe preocuparte. Como yo ya ví el resultado sé que el rozamiento es mayor que F. Una relación completamente anti-intuitiva de la que volveremos a charlar al final. Pero, te repito, eso viene después, lo tuyo es sólo dirección y sentido, ahí no podés errarle.

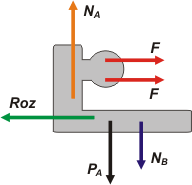Vamos al cuerpo A que es un poco más complicado. Tenemos su peso, PA. Tenemos la fuerza que B hace sobre A, NB. Y tenemos el apoyo con el suelo, NA.

Vamos a las fuerzas horizontales. Salen dos sogas tensas hacia la derecha. Cada una realiza la misma fuerza (por tratarse de una cuerda ideal) de modo que marchen 2 F. El bloque B realiza una fuerza de rozamiento hacia la izquierda que no es otro que el par de interacción de la que actúa sobre él, de modo que no hay que ponerle un nombre diferente, vuelve a ser Roz.

   

Ahora podemos ir a las ecuaciones de Newton. Tené en cuenta que si el enunciado nos obliga a que los cuerpos no deslicen entre sí, entonces, las aceleraciones de ambos cuerpos será la misma:

    
pieza en L (eje x) →   ΣFx = mA ax   →     2 F — Roz = mA . a [1]
bloque (eje x) →   ΣFx = mB ax →         Roz — F = mB . a [2]
pieza en L (eje y) →   ΣFy = mA ay →  NA — PA — NB = 0 [3]
bloque (eje y) →   ΣFy = mB ay →          NB — PB = 0 [4]
   
Todavía nos queda por plantear una ecuación más. Acordate que para darle el gusto al enunciado, el rozamiento debe ser el máximo posible:    
Rozamiento →     →            Roz = µe NB [5]
   

La ecuación [3] no aporta nada, y podemos olvidarla. Pero las otras 4 las metemos en la licuadora algebraica y encontramos la solución.

Metemos la [4] en la [5] y resulta que...

Roz = µe . PB = 0,30 . 60 N =

Roz = 18 N

Podemos multiplicar por 2 la ecuación [2] y lo que da lo sumamos con la [1].

Roz = mA . a + 2 . mB . a

Roz = a (mA + 2 . mB )

Despejamos a:

    
a =   Roz  
mA + 2 . mB
   
a =   18 N  
10 kg + 12 kg
   
  a = 0,82 m/s²  
   
Con ese valor volvemos a las dos ecuaciones [1] y [2] y verificamos en en ambas obtenemos el mismo valor para F.    
  F = 13,09 N  
   

DISCUSION: Lo que tiene de interesante este ejercicio es que muestra un dispositivo que le plantea trampas a la intuición: ¿cómo puede ser que la fuerza de rozamiento, que es la que acelera al cuerpo B, sea mayor que la fuerza que hay que ejercer desde afuera? Si sufrís de insomnio te recomiendo que olvides esa pregunta. Vamos a una discusión más sencilla: si considerásemos a todo el dispositivo como un solo cuerpo, la única fuerza externa es F y la aceleración no tiene más remedio que respetar:

 F = mtot . a

Afortunadamente, éso es justamente lo que dicen nuestros números, de modo que podemos irnos a la cama sabiendo que el único motivo para nuestro insomnio será el funcionamiento de este maldito dispositivo.

   
DESAFIO: Supongamos que se ejerce una fuerza de 10 N, ¿cuánto valdría la aceleración de cada cuerpo?  
Algunos derechos reservados. Se permite su reproducción bajo la solemne promesa de citar la fuente. Última actualización mar-10. Buenos Aires, Argentina.