 |
NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
|
|

|
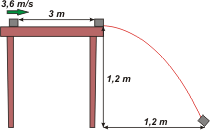
NMS d2.17* - Un bloque se desplaza sobre una mesa de 1,2 m de altura. Hay rozamiento entre el bloque y la mesa. Al pasar por un punto distante 3 m del borde tiene una velocidad de 3,6 m/s, como indica la figura. Abandona la mesa y golpea en el suelo en un punto situado a 1,2 m del borde de la mesa.
a) ¿cuánto vale el coeficiente de rozamiento dinámico entre la mesa y el bloque?
b) ¿cuánto vale el módulo de la velocidad del bloque cuando llega al piso? |
 |
|
Un lindo ejemplo de cuco. A los chicos les asustan los cucos... a los grandes les dan gracia. Los ejercicios combinados tienen fama de cucos (ya sabés para quién). Combinado, porque arriba de la mesa transcurre un fenómeno de rozamiento, que habrá que resolver con consideraciones dinámicas. Pero para resolverlo necesitarás conocer la aceleración de ese movimiento, arriba de la mesa. Para encontrar esa aceleración tendrás que conocer con qué velocidad llega al borde (la misma con la que el bloque sale despedido). Y para hallar esta última tendrás que resolver el tiro horizontal que se desarrolla afuera de la mesa.
Es largo -lo admito- pero no difícil. Empecemos con la cinemática. |
|
|
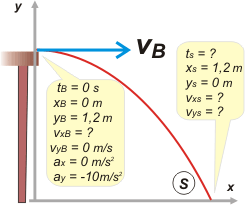 |
Espero que tengas los modelos de ecuación horaria a mano... En ellos reemplazamos las constantes del movimiento (del borde de la mesa, B) y nos quedan así:
x = vB . t
y = 1,2 m – 5 m/s² . t²
vy = – 10 m/s² . t
A esas ecuaciones les pedimos que hablen del instante S, cuando el bloque llega al suelo. |
|
|
|
Y ellas dicen:
1,2 m = vB . tS
0 m = 1,2 m – 5 m/s² . tS²
vyS = – 10 m/s² . tS
Si te fijás... hay ahí tres ecuaciones con tres incógnitas... de modo que podés resolver el sistema y hallarlas. Esta vez no te ayudo, porque si no, el ejercicio se me hace muy largo.
tS = 0,49 s
vB = 2,45 m/s
Esta es la que nos sirve para el asunto del rozamiento y también para conocer la velocidad al llegar al suelo... porque la velocidad horizontal se mantiene constante.
vyS = 4,9 m/s
Esta también nos sirve para calcular la velocidad justo al llegar al suelo. Para calcularla tenemos que componer ambas, por pitágoras.
vS = (2,45² + 4,9²)1/2 m/s
|
|
|
| |
vS = 5,48 m/s |
respuesta b) |
|
|
|
| Seguimos con cinémática, pero ahora... arriba de la mesa. Otro esquema. |
|
|
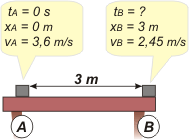 |
Usé un nuevo SR (espero que no te ofendas). Acá tenés un MRUV, en el que nos falta la aceleración. Las ecuaciones son éstas:
x = 3,6 m/s . t + ½ a . t²
v = 3,6 m/s + a . t
Vamos a pedirles que hablen del borde, B:
|
|
|
|
Y ellas dicen:
3 m = 3,6 m/s . tB + ½ a . tB²
2,45 m/s = 3,6 m/s + a . tB
Y nuevamente aparecen dos incógnitas. Acá el álgebra es un poquito más ardua... pero para vos no va a ser problema. El resultado que nos interesa es:
a = – 1,16 m/s²
Ahora sí, podemos ir a la dinámica del rozamiento... ¡Hay que hacer un DCL! |
|
|
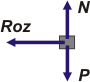 |
(eje x) → ΣFx = m ax → — Roz = m a
(eje y) → ΣFy = m ay → N — P = 0 |
|
|
|
El resto es pavada...
Roz = μd . N
— m . a = μd . P
— m . a = μd . m . g
— a = μd . g
μd = — a /g
μd = — (— 1,16 m/s²) / 10 m/s²
|
|
|
| |
μd = 0,116 |
respuesta a)... ¡llegamos! |
|
|
|
| |
|
|
DISCUSION: Cada pedazo de ejercicio, en sí mismo, es bastante sencillo. De cada tema en esta guía los hubo más difíciles. Lo original que aporta éste es el encadenamiento de cada parte. Para hacerlo de un tirón tenés que acertar cuál de las tres partes se resuelve por sí sola y cuál no se resuelve hasta que tenés el dato que te aporta el otro. Con un poco de experiencia te das cuenta por dónde empezar y por cuál continuar. Pero aún si no acertaras... el ejercicio completo sale igual, teniendo el temple de dejar los resultados de cada etapa expresados correctamente con un símbolo claro que no se pierda ni entrevere... por ejemplo vB. |
|
 |
| *Este ejercicio fue parte del examen parcial de Física tomado el 19 de mayo de 2009 en Ciudad Universitaria. |
|
|
| DESAFIO: ¿En qué cambian los resultados si la distancia recorrida sobre la mesa es de 1 m? |
|
| Algunos derechos reservados.
Se permite su reproducción nadando en la fuente. Última actualización may-09. Buenos Aires, Argentina. |
|
|
|

