NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
|
|

|
d2.14- De una pila de tablones, que pesan
100 Newton cada uno, se quiere retirar el quinto
(contando desde arriba). Calcular la intensidad
mínima que deberá tener la fuerza horizontal capaz
de ponerlo en movimiento, y qué fuerza habrá
que aplicar al conjunto de los cuatro restantes,
para que no lo acompañen.
¿Qué fuerza deberá aplicarse, para extraerlo a
velocidad constante, después que arrancó?
Datos: μe= 0,6 ; μd= 0,4. |
| ¿Para qué tantos tablones, si no los voy contar? Te propongo una trampita... chiquita... nada del otro mundo: vamos a soldar los cuatro tablones de arriba y considerarlos como un único cuerpo, ¿te parece? El peso de ese cuerpo hipotético (formado por cuatro tablones) vale 400 N. Abajo de él está el quinto, pobrecito, todo aplastado. Pero peor la pasa el de abajo, el 6to, que soporta al peso de los cuatro de arriba y al 5to también. Acá va un esquema. |
|
|
 |
Ahí tenés: los cuatro de arriba amalgamados, el 5to. le sigue, y abajo agregué algunos más... que ni pinchan ni cortan, da lo mismo que sea uno, dos, o veintitrés.
Ahora organicémonos con el ejercicio: se habla de dos fuerzas, una aplicada sobre el 5to. tablón, F5to (la voy a poner hacia la derecha), y otra sobre el grupo de arriba, Far (hacia la izquierda, para que no se venga con el 5to.). |
|
|
|
También hay dos momentos: el primero, una situación estática, en la que buscaremos la mínima fuerza necesaria para arrancar al 5to. tablón de la pila... en ese caso las fuerzas de rozamiento que hay que superar serán las de rozamiento estático máximo... la que se calcula con los coeficientes de rozamiento estático.
El segundo momento es la situación dinámica en la que tenemos que imaginar al tablón saliendo a velocidad constante después de haber sido liberado de su estancamiento. Las fuerzas que hay que aplicar en este segundo momento serán diferentes a las del primero, ya que las fuerzas de rozamiento implicadas serán de tipo dinámico.
Como las fuerzas hay que aplicarlas sobre dos cuerpos diferentes, necesitamos dos DCLs. Ahora viene lo más importante del ejercicio. Acá van: |
|
|
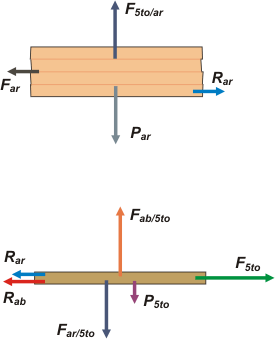 |
Veamos si te cierran: sobre el bloque de arriba actúan cuatro fuerzas. Las verticales son fáciles: el peso del conjuto, Par, y la fuerza con la que el 5to. tablón lo sostiene, F5to/ar, esa fuerza que vos llamarías -tontamente- normal. Las horizontales son: la fuerza que nos pregunta el ejercicio, que hay que hacer sobre estos cuatro tablones para que no salgan acompañando al 5to., Far, y la fuerza de rozamiento con la que el 5to. tablón pretende arrastrar al conjunto cuando nos lo llevamos de la pila, Rar.
Ahora vamos al DCL del 5to. tablón. Las verticales son: el peso, P5to; la fuerza con la que el conjunto de arriba aplasta al 5to., Far/5to, (otra normal); y la fuerza con la que los de abajo sostiene al 5to., Fab/5to (¡otra normal más!). Y las horizontales son: la fuerza que hay que hacerle para sacarlo de ahí, F5to; el rozamiento en la cara de abajo, Rab; y el rozamiento en la cara de arriba, Rar. |
|
|
| Si sos de los que se resisten a utilizar subíndices... estás en el horno |
|
Algunas fuerzas que acabo de mencionar son pares de acción y reacción. Es muy importante identificarlas, ya que cuando las ponga a jugar el partido del sistema de ecuaciones no tienen que pasar por dos diferentes cuando son una misma. Te dejo a vos que las identifiques, total, como fui sistemático para nombrarlas (en lugar de ponerles nombres de fantasía y equívocos: como normal) se convierte en una tarea de niños. |
|
|
Conj. arr.
5to. tablón |
→
→
→
→ |
ΣFx = 0 →
ΣFy = 0 →
ΣFx = 0 →
ΣFy = 0 → |
Rar — Far = 0
F5to/ar — Par = 0
F5to — Rar — Rab = 0
Fab/5to — Far/5to — P5to = 0 |
[1]
[2]
[3]
[4] |
|
|
|
Todavía nos queda plantear lo que sabemos de las fuerzas de rozamiento estáticas máximas... y en este ejercicio se trata de la parte más difícil (ésta es la parte más interesante del problema). Lo que dice la ley y muy pocos docentes te explican es que esa fuerza de rozamiento entre dos superficies es igual al producto entre el coeficiente de rozamiento de ese par de superficies por la fuerza que las comprime.
En lugar de explicarte eso, te dicen: "por la normal", (¡quisiera matarlos!). |
|
|
Rozamientos |
→
→ |
Rar = μe . Far/5to
Rab = μe . Fab/5to |
|
[5]
[6] |
|
|
|
Ahora sí, si tenés ganas, contá las incógnitas y vas a ver que el problema encuentra solución. Yo te lo hago, no llores. De la ecuación [2] sale:
F5to/ar = 400 N
Meto eso en la [4] y queda:
F5to/ab = 500 N
Hasta acá son puras obviedades. Pero ahora metemos esto en la [5] y la [6]...
Rar = 240 N
Rab = 300 N
Finalmente reemplazamos los rozamientos en las ecuaciones [1] y [3] |
|
|
| |
Far = 240 N y F5to = 540 N |
|
|
|
|
La segunda etapa, la dinámica, es casi idéntica a esta primera porque tampoco hay aceleraciones y las ecuaciones son exactamente las mismas salvo que el coeficiente de rozamiento será el de tipo dinámico. Te lo dejo a vos.
Comentario: Si este ejercicio tiene una enseñanza peculiar consiste en la siguiente. Cuando te dicen:
Roz = μ . N
N, normal (palabra nefasta en la enseñanza de la Física) es la fuerza que comprime a las superficies en rozamiento. Si te cuesta ubicarla, imaginate que sos una pulga metida entre esas dos superficies y buscá al culpable de tu aplastamiento. En nuestro ejercicio: si tu ubicación pulgosa fuera la cara superior del 5to. tablón no deberías tener inconveniente en culpar a la fuerza entre el 5to. tablón y el conjunto de arriba, F5to/ar. Y si estuvieras en la cara de abajo también acertarías. Pulga sí, pero tonta no. |
|
|
| DESAFIO: ¿Cuánto valdrían las cuatro fuerzas que se preguntan en este ejercicio si todo el conjunto estuviese cayendo libremente en el vacío? |
|
 |
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Está absolutamente prohibido utilizar este material sin antes haber hecho un intento por resolver es problema sin ayuda. Severas penalizaciones a los infractores. Última actualización ene-08. Buenos Aires, Argentina. |
|
|
|

