NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Leyes de Newton)
|
|

|
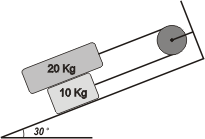
NMS 1. 46* - En el sistema de la figura un bloque de 20 kg desliza sobre otro de 10 kg. Entre ambos bloques, y entre el cuerpo de 10 kg y el plano, el rozamiento es despreciable. Considere la soga inextensible y de masa despreciable, y la polea sin masa y su garganta perfectamente lisa. Determinar:
a) el vector aceleración del cuerpo de 10 kg.
b) la tensión en la cuerda. |
 |
|
| |
| Bien... esto es terrible. Pero igualmente vamos a empezar por los correspondientes DCL. Como tenemos dos cuerpos, tendremos dos DCLs. |
|
|
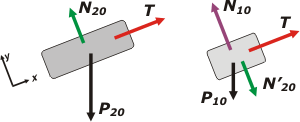 |
Acá los tenés. A la fuerza que hace la cuerda en cualquiera de los extremos le puse el mismo nombre, T, ya que es una de las características de las cuerdas sin masa: hacen la misma fuerza en ambos extremos. |
|
|
|
La fuerza que llamé N20 es la fuerza de contacto entre el bloque de arriba y el de abajo. Yo le hubiera puesto otro nombre, por ejemplo: F10/20. Su par de interacción aparece aplicado sobre el otro bloque (le puse el mismo color) y la llamé N'20. El nombre "orgánico" habría sido F20/10. No es fácil remar todo el tiempo contra la corriente.
También está la fuerza de contacto entre el plano inclinado y el bloque de abajo, N10. Y los pesos. Es obvio que vamos a descomponer los pesos y reemplazarlos por sus componentes. Te recomiendo hacerlo en DCLs aparte. Rehacelos. Este ejercicio lo tomamos en un examen, y no te explico la cantidad de errores cometidos por la vagancia de no rehacer los DCL. |
|
|
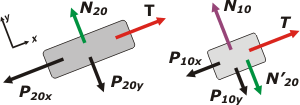 |
Ahora sí, está todo listo para escribir las ecuaciones de newton para ambos bloques para ambas direcciones. Fijate que voy a utilizar el mismo SR para ambos bloques... de modo que una de las aceleraciones deberá ser negativa (obviamente la del bloque más grande, que debe acelerar para abajo). |
|
|
|
| Nos quedan así: |
|
|
| bloque de 20 (eje x) |
→ ΣFx = m20 ax |
→ T — P20x = — m20 . a |
[1] |
| bloque de 10 (eje x) |
→ ΣFx = m10 ax |
→ T — P10x = m10 . a |
[2] |
| bloque de 20 (eje y) |
→ ΣFy = m20 ay |
→ N20 — P20y = 0 |
|
| bloque de 10 (eje y) |
→ ΣFy = m10 ay |
→ N10 — N'20 — P10y = 0 |
|
|
|
|
Las ecuaciones en y, en este caso no aportan gran cosa, ya que al no haber rozamientos (qué palabra despreciable) ni preguntas sobre las fuerzas que actúan en ese eje... no vamos a usarlas. pero las de x sí.
No te olvides que:
P20x = m20 . g . sen 30° = 100 N
P10x = m10 . g . sen 30° = 50 N
Estamos listos para hacer cálculos. Un método rápido es restar miembro a miembro las ecuaciones [2] — [1]. Quedan así:
T — P10x — (T — P20x ) = m10 . a — (— m20 . a)
P20x — P10x = a . (m20 + m10 )
Despejamos la aceleración:
|
|
|
| a = |
|
P20x — P10x |
|
|
| m20 + m10 |
|
|
|
| a = |
|
100 N — 50 N |
|
|
| 20 kg + 10 kg |
|
|
|
|
|
|
|
|
|
| Con ese valor volvemos a las dos ecuaciones y verificamos que la tensión nos dé el mismo resultado en ambas. Efectivamente: |
|
|
|
|
|
DISCUSION: Volvé a mirar la primera ecuación en la que aparece la aceleración: |
|
 |
| |
| a = |
|
P20x — P10x |
|
|
| m20 + m10 |
|
|
|
|
| Jugá un cacho cambiando los valores de las masas de los bloques... por ejemplo que ambas valgan los mismo, que una de ellas valga cero... verás que llegás a resultados predecibles e intuitivos. Eso te indica que esa expresión describe efectivamente el sistema. |
|
| *Este ejercicio perteneció al primer examen de Física tomado el 19 de mayo de 2009 en Ciudad Universitaria y otras sedes del CBC. |
|
|
| DESAFIO: ¿Te animás a agregar un pequeño rozamiento dinámico... digamos de un coeficiente de 0,1 en todas las superficies? |
|
| Algunos derechos reservados.
Se permite su reproducción bajo la solemne promesa de citar la fuente. Última actualización may-09. Buenos Aires, Argentina. |
|
|
|

