NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
Cuerpos vinculados
|
|

|
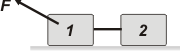
| NMS 1.42 - En el sistema de la figura, la masa del cuerpo 1 vale 8 kg, La fuerza forma 30 grados con la horizontal y su módulo vale 50 N. ¿Cuál debía ser el valor de la masa del cuerpo 2 para que la aceleración del conjunto sea 1 m/s²? |
 |
|
|
|
|
Como siempre, tenemos que empezar confeccionando los diagramas de cuerpo libre. Tratándose de dos cuerpos, serán dos diagramas. |
|
|
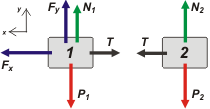 |
Los largos de las flechas no son exactos, generalmente en los DCL no tenemos en cuenta el módulo de las fuerzas y lo usamos, sobre todo, para detectar y analizar la dirección y sentido de las fuerzas.
Vamos, entonces, cada una de ellas. |
|
|
|
Sobre el cuerpo 2 actúan 3 fuerzas: su peso, P2, su apoyo sobre el plano, N2, y la fuerza con que lo tracciona la soga, T.
Sobre el cuerpo 1 actúa la soga, T (que no lleva subíndice porque suponemos que la soga es ideal y por lo tanto ejerce idénticas fuerzas en ambos extremos), el peso, P1, el apoyo, N2, y la fuerza F que para ahorrar tiempo ya la presenté como desdoblada en sus componentes Fx y Fy. |
|
|
| Vamos a las ecuaciones de Newton. Empecemos por el cuerpo 1. |
| |
ΣFx = m1 ax → |
Fx — T = m1 a |
[1] |
|
| |
ΣFy = m1 ay → |
N1 + Fy — P1 = 0 |
[2] |
|
| Seguimos con el cuerpo 2. |
|
|
|
| |
ΣFx = m2 ax → |
T = m2 a |
[3] |
|
| |
ΣFy = m2 ay → |
N2 — P2 = 0 |
[4] |
|
|
|
|
A su vez, las componentes horizontal y vertical de la fuerza F valen:
Fx = F cos 30º
Fy = F sen 30º
En este ejercicio, las ecuaciones [2] y [4] no aportan nada. En las otras dos, en cambio, se halla la solución. Meto la [3] en la [1]:
Fx — m2 a = m1 a
Y despejo m2:
m2 a = — m1 a + F cos 30º
m2 = — m1 + F cos 30º / a
m2 = — 8 kg + 50 N 0,866 / 1 m/s²
|
|
|
|
|
|
| |
|
|
DESAFIO: ¿Qué valor mínimo debe tener la fuerza para que el conjunto se desplace a velocidad constante? |
|
 |
| Algunos derechos reservados.
Se permite mimeografiarlo (?) citando la fuente. Última actualización
may-11. Buenos Aires, Argentina. |
|
|
|

