NO ME SALEN
EJERCICIOS RESUELTOS DE FÍSICA
(Leyes de Newton, cuerpos vinculados)
|
|

|
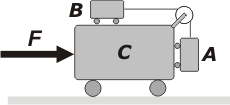
NMS 1.40* - El sistema mecánico de la figura consta de tres coches de
masas mA = 0,3 kg, mB = 0,2 kg y mC = 1,5 kg, respectivamente. Si la fuerza F que está actuando sobre el coche C en sentido horizontal
es tal que los coches A y B permanecen en reposo respecto de C, calcular
el módulo de F y la tensión de la cuerda. Considere que la polea y la cuerda (inextensible) tienen masa despreciable, y qe todos los rozamientos son también despreciables.
|
 |
|
|
*Este ejercicio formó parte de la prueba de la Olimpíada Internacional de Física, Checoslovaquia, 1969.
Pero qué pretenden, ¡¿que resuelva un ejercicio de una olimpíada?! Eso es sólo para genios, para gente que sabe mucha... mucha Física... además miren qué sistema complicado...
Dejá de llorar. Es cierto que los ejercicios de olimpíadas suelen ser difíciles. Vas a ver que aplicando el método... ¡el ejercicio sale solo!
¿Y por dónde empezamos? Como SIEMPRE... ¡por los diagramas de cuerpo libre (DCL)!
Ahí está la clave, ya lo sabés: no comerse ni inventar fuerzas. En cada contacto entre cuerpos aparece un par de interacción. Si para nombrar a las fuerzas usán nombres "orgánicos" (FAC sería al fuerza que A le hace a C) no podés equivocarte. |
|
|
 |
|
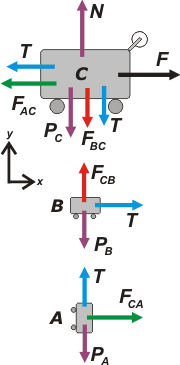
Las fuerzas que actúan sobre C son siete: su propio peso, PC; la fuerza exterior F que acelera al conjunto; la fuerza con que el piso lo sostiene, N; la fuerza que B le hace a C, FBC; la fuerza que A le hace a C, FAC y la tensión de la cuerda, T, que actúa sobre el brazo de la polea (que es parte del carro C) tirando hacia abajo y hacia la izquierda.
Las fuerzas que actúan sobre B son sólo tres: su propio peso, PB; la fuerza con que lo tira la soga, T y la fuerza con que lo sostiene C, FCB.
Las fuerzas que actúan sobre A también son sólo tres: su propio peso, PA; la fuerza con que lo sostiene la soga, T y la fuerza con que lo empuja C, FCA.
Fijate que los nombres orgánicos que les puse a las fuerzas acusan su naturaleza de par de interacción. Para que los puedas identificar fácilmente los dibujé con un mismo color para cada par.
Si pudiste hacer esto bien, el resto es pan comido. Toda la dificultad estaba aquí, lo que sigue es muy mecánico.
Como todos los ejercicios de dinámica, después de hacer los DCL, continuamos por las ecuaciones de Newton (son dos para cada cuerpo). |
|
|
|
| Como el conjunto acelera todo junto y sin movimiento relativo entre los cuerpos, todos tienen la misma aceleración, que llamaré a. |
|
|
| Coche C (eje x) |
→ |
ΣFx = m ax |
→ |
F — FAC — T |
= mC . a |
[1] |
| Coche B (eje x) |
→ |
ΣFx = m ax |
→ |
T |
= mB . a |
[2] |
| Coche A (eje x) |
→ |
ΣFx = m ax |
→ |
FAC |
= mA . a |
[3] |
| Coche C (eje y) |
→ |
ΣFy = m ay |
→ |
N — PC — FBC — T |
= 0 |
[4] |
| Coche B (eje y) |
→ |
ΣFy = m ay |
→ |
FBC — PB |
= 0 |
[5] |
| Coche A (eje y) |
→ |
ΣFy = m ay |
→ |
T — PA |
= 0 |
[6] |
|
|
|
Sabés que dadas las masas también tenés que considerar como dato los pesos... de modo que si contás bien, tenemos 6 ecuaciones y 6 incógnitas (las puse en rojo para facilitarte la cuenta). O sea... ¡ya resolvimos la física del ejercicio de la olimpíada!¡Somos unos genios! El resto es álgebra y ya tiene menos interés. Pero igual te lo resuelvo para que no me andes criticando por ahí.
Las ecuaciones [4] y [5] no las voy a usar ya que hablan de incógnitas que no nos interesan ni nos pide el enunciado. Las otras sí. De la [6] despejo T y la calculo:
T = PA
T = mA . g
T = 0,3 kg . 10 m/s²
|
|
|
|
|
|
Con ese valor voy a la [2] y calculo la aceleración:
a = T / mB
a = 3 N / 0,2 kg
a = 15 m/s²
Paso a la [2] y calculo la fuerza de contacto entre A y C:
FAC = mA . a
FAC = 0,3 kg . 15 m/s²
FAC = 4,5 N
Con estos valores voy a la [1], despejo F y la calculo.
F = mC . a + FAC + T
F = 1,5 kg . 15 m/s² + 4,5 N + 3 N
|
|
|
|
|
|
No fue el más elegante de los desarrollos algebraicos. No queda bien realizar cálculos intermedios, y en general no lo hago. Pero acá lo hice en pos de la economía y la claridad para los inexpertos.
Fijate lo siguiente: si hubiéramos considerado al conjunto como un cuerpo sólido, sin articulaciones internas, su masa sería de 2 kg (la suma de las 3 masas que lo forman) y la única fuerza externa que lo acelera es F. Luego, debe cumplirse que esa fuerza debe ser igual al producto de la masa por la aceleración, y así ocurre:
30 N = 2 kg . 15 m/s²
Siempre hay que tener a mano esas ideas generalizadoras y simplificadoras que nos ayudan a supervisar el resto de los razonamientos. |
|
|
| NOTA: tomado y adaptado de http://www.exploralaciencia.profes.net/ver_galeria_enlaces.aspx?id=11329 |
|
|
 |
| DESAFIO: Si desapareciera la fuerza F, ¿cuánto valdría la aceleración de cada coche? |
|
| Algunos derechos reservados.
Se permite tu reproducción recitando en la fuente. Última actualización jul-12. Buenos Aires, Argentina. |
|
|
|

