NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Leyes de Newton)
|
|

|
NMS 1.30* - Una máquina tira de una cuerda para levantar verticalmente un cuerpo de masa m = 12 kg, de manera que la velocidad del mismo aumenta uniformemente de 0 a 6 m/s en los primeros 3 segundos, luego se mantiene constante durante 5 segundos, y finalmente disminuye a razón de 3 m/s cada segundo durante dos segundos.
a) Graficar la altura del cuerpo en función del tiempo.
b) Graficar la tensión de la cuerda como función del tiempo. |
| * Este ejercicio formó parte del primer examen parcial de Física del CBC tomado en noviembre de 2012. Para ver el tema de examen completo hacer click acá. |
|
|
Bien, tenemos acá un ejercicio que tiene una parte de cinemática y otra de dinámica.
Te planto el gráfico que se pide en el ítem a) y paralelamente te cuento cómo lo hice.
|
| |
|
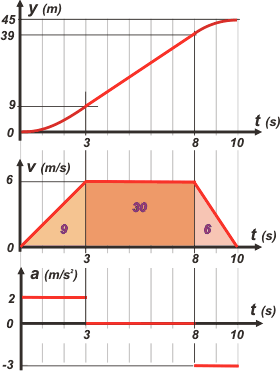 |
El de arriba es el que pide el enunciado. Pero la clave está en el del medio, el de velocidad en función del tiempo.
Ese es muy sencillo de hacer ya que no hace más que contar lo mismo que describe el enunciado.
Pero una vez hecho se hace muy sencillo conocer los desplazamientos realizados en cada tramo, basta con obtener las áreas encerradas en cada tramo de curva.
Es un hecho que no tenés que olvidar nunca: el área encerrada bajo la curva de un gráfico v vs. t representa el desplazamiento correspondiente.
Se trata de un par de triángulos y un rectángulo... no hace falta que te recuerde cómo calcular el área de esas figuras.
De paso grafiqué las aceleraciones... No me salen no puede con su genio. |
|
|
|
El encolumnamiento y el orden en que se encuentran los gráficos no es un capricho, y tiene su lógica. Acá siempre los vas a encontrar dispuestos de la misma manera, que hemos denominado tándem.
Lógicamente, también podrías haber llegado a los mismos valores de posición utilizando las ecuaciones horarias de cada tramo. Habría sido más trabajoso pero no viene mal que lo practiques. Acá te consigno las ecuaciones. Aprovechá y analizalas.
de 0 a 3 s, MRUV → y = 1 m/s² t²
de 3 a 8 s, MRU → y = 9 m + 6 m/s ( t – 3 s)
de 8 a 10 s, MRUV → y = 39 m + 6 m/s ( t – 8 s) – 1,5 m/s² ( t – 8 s)²
Para responder la segunda pregunta (acá sí estamos en la dinámica) tenemos que hacer un DCL. |
|
|
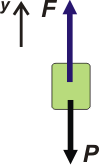 |
F es la fuerza que hace la máquina que tira para arriba. Es obvio que si es mayor que el peso, P, acelerará hacia arriba (como en el primer tramo), si es igual al peso la aceleración valdrá cero (como en el segundo tramo) y si es menor que el peso tendrá una aceleración hacia abajo (como en el tercer tramo).
Para conocer los valores exactos hay que recurrir a la segunda ley de Newton: ΣF = m . a.
Y lo hacemos tramo por tramo. Tomemos un sistema de referencia hacia arriba para ser coherentes con lo anterior. |
|
|
|
de 0 a 3 s → F(0-3) – 120 N = 12 kg . 2 m/s²
de 3 a 8 s → F(3-8) – 120 N = 0
de 8 a 10 s → F(8-10) – 120 N = – 12 kg . 3 m/s²
Así obtenemos:
F(0-3) = 144 N
F(3-8) = 120 N
F(8-10) = 84 N
Volquémoslo en un gráfico, como pide el enunciado. |
|
|
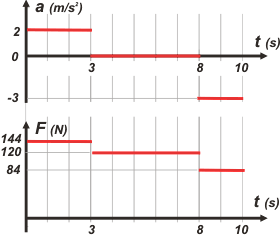 |
Es el de abajo, obviamente, pero me gustó la idea de mostrártelo junto con el de aceleración (el mismo que aparece allá arriba). En tándem.
Fijate que son semejantes, sólo que hay un cambio de escala, y un corrimiento de 120 N, que es lo que vale el peso del objeto.
Podría haber sido más detallista... pero no quise que me odies. Lo dejé en un término medio. Pero creeme, en un examen este ejercicio no debe demandarte más de cinco minutos. |
|
|
 |
DESAFIO: ¿cuánto vale la velocidad media de todo el ascenso? |
|
| Algunos derechos reservados.
Se permite tu reproducción recitando en la fuente. Última actualización jul-14. Buenos Aires, Argentina. |
|
|
|

