NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Leyes de Newton, dinámica del movimiento circular)
|
|

|
 |
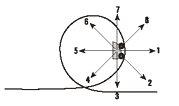
NMS 1.27- Un carrito de montaña rusa ejecuta un
rizo y se encuentra en la posición que indica la figura. ¿Cuál de todos los vectores dibujados representa
la fuerza neta que actúa sobre el carrito
en ese instante? |
|
 |
|
| Por supuesto, y como siempre, el mejor modo de empezar a resolver este ejercicio (como cualquier otro de dinámica) es con un DCL. Vas a ver que si hacemos el DCL correctamente -lo que es muy fácil- el problema sale con fritas. |
|
|
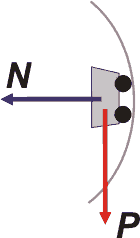 |
Discutamos si son esas dos que indiqué en el DCL las únicas fuerzas que actúan sobre el carrito.
Como está cerca de la superficie terrestre está sometido a su atracción gravitatoria. A esa fuerza la llamamos vulgarmente peso, P, y es vertical. Sobre ella no hay dudas, ¿estamos?
El único objeto con el que carrito está en contacto es la vía, los rieles. Estos, indudablemente, realizan una fuerza sobre el carrito. Esa fuerza de contacto, debe ser perpendicular (normal, si te gusta más) a la superficie de las vías. No le cabe otra posibilidad que apuntar hacia el centro de la curva. De hecho es la fuerza que lo obliga a doblar hacia la izquierda (tuya).
No hay ningún otro cuerpo actuando sobre el carrito, por lo tanto, no hay más fuerzas |
|
|
|
| Prácticamente tenemos cocinado el asunto. El enunciado pregunta sobre la fuerza neta, o sea sobre la sumatoria de todas las fuerzas que actúan, o sea pregunta por la composición de éstas únicas dos. Hay una sola respuesta posible. |
|
|
| |
el vector que representa la fuerza neta es el 4 |
|
|
|
|
| |
|
|
DISCUSION: Siempre tenés que tener presente, en cada momento de tu vida, en cada instante sin excluir ninguno, la 2da. ley de la dinámica, o ley de Newton, o principio de la masa. Llamalo como quieras, pero es éste: 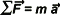 . .
En este caso mirá lo que nos dice... sea cual sea la masa del carrito la aceleración y la fuerza neta tienen siempre la misma dirección y sentido. O sea que la aceleración del carrito también debe estar representado por un vector como el 4. Con la misma dirección y sentido. Acordate que aceleración es la magnitud que indica el cambio de velocidad, o sea, que si interpretamos ese vector, lo que nos dice es cómo se está moviendo el carrito. Para interpretarlo mejor siempre conviene descomponerlo en dos direcciones: una tangencial (que lleva la misma dirección que la velocidad) y otra ortogonal a la velocidad (con perdón de la palabra). La tangencial me dice si va más rápido o más lento y la perpendicular, si está doblando.
En nuestro caso debemos concluir que el carrito está disminuyendo la velocidad (si está subiendo) o aumentando su velocidad (si está bajando) y doblando a la izquierda (en cualquier caso). ¡Chocolate por la noticia! (El Peso es la que lo frena si sube o empuja si baja, y las vías las que lo hacen doblar). |
|
 |
| DESAFIO: Supongamos, para este problema, que agregamos rozamiento... ¿podrían (haciendo cualquier tipo de suposición adicional que se te ocurra...) los vectores 5 o 6 representar la fuerza neta? ¿Podría el 7, el 8, el 1, el 2 o el 3 representar la fuerza neta? |
|
| Algunos derechos reservados.
Se prohibe su no su reproducción citando la fuente. También está prohibido fumar marihuna en coches y andenes. Última actualización oct-06. Buenos Aires, Argentina. |
|
|
|

