NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Leyes de Newton, cuerpos vinculados)
|
|

|
 |
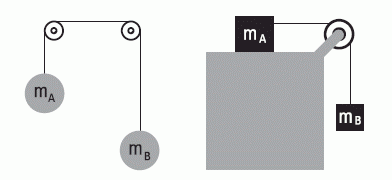
NMS 1.20- Los cuerpos unidos por una soga de masa
despreciable se hallan en reposo. ¿Cómo evolucionarán
los sistemas? (se desprecia el rozamiento).
Caso A: mA = mB
Caso B: mA = 10 kg; mB = 1 kg
|
 |
| |
|
Estos ejercicios combo... tenemos cuatro casos: dos para el sistema de la izquierda y dos para el sistema de la derecha.
Empecemos con el de la izquierda. El hecho de que existan dos poleas no agrega nada importante; no te olvides que las poleas (en este curso) sólo sirven para desviar la dirección de las cuerdas, no cambian aceleraciones ni modifican la intensidad de las fuerzas.
Vamos a los DCLs. |
|
|
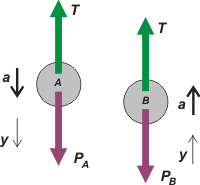 |
Sobre cada cuerpo actúan sólo dos fuerzas, su porpio peso y la fuerza que hace la soga, que llamaré tensión, T.
Por tratarse de una soga ideal no tiene masa, eso garantiza que la fuerza que realiza en ambos extremos es la misma (por eso no le puse subíndice).
Y por ser inextensible la aceleración de ambos cuerpos es la misma... eso sí: si en un cuerpo apunta hacia arriba, en el otro debe apuntar hacia abajo. Cuál con cuál, es indistinto, lo elige cada quién. |
|
|
|
OK, vamos a las ecuaciones.
Cuerpo A → ΣFy = mA . a → PA — T = mA . a [1]
Cuerpo B → ΣFy = mB . a → T — PB = mB . a [2]
Es mentira, no puede ser tan fácil... dadas las masas, se convierte en un sistema de 2 ecuaciones con dos incógnitas.
Sumo miembro a miembro [1] y [2]
PA — T + T — PB = mA . a + mB . a
en el primer término se cancela T y en el segundo saco factor común a
PA — PB = ( mA + mB ) . a
recuerdo que P = m . g
mA . g — mB . g = ( mA + mB ) . a
saco factor común g y despejo a: |
|
|
|
|
|
| Recién ahora hacemos números. En el caso A, en el que las masas son iguales... |
|
|
|
|
|
| En el caso B, mA = 10 kg; mB = 1 kg |
|
|
|
|
|
| Ahora vamos al sistema de la derecha B (es un clásico). Tenemos que hacer dos DCLs. |
|
|
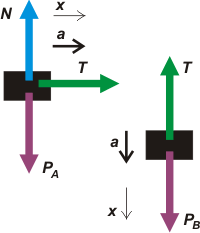 |
Fijate que adopté para ambos cuerpos un SR coherente (la dirección de movimiento, sea cual sea tendrá el mismo signo).
Para el cuerpo A no cambia casi nada, solo que ahora tira de la soga, T, que es la misma que sostiene al cuerpo B.
Naturalmente, se vienen las ecuaciones de Newton. |
|
|
|
Cuerpo A → ΣFx = mA ax → T = mA a
Cuerpo B → ΣFx = mB ax → PB — T = mB a
Hay dos ecuaciones con dos incógnitas. De modo que podemos calcular la aceleración. Un método sencillo y rápido es sumar miembro a miembro las dos ecuaciones y luego despejar a.
a = PB / ( mA + mB )
|
|
|
|
|
|
Recién ahora hacemos números. En el caso A, en el que las masas son iguales... |
|
|
|
|
|
| En el caso B, mA = 10 kg; mB = 1 kg |
|
|
|
|
|
| |
|
|
| DESAFIO: En el enunciado te cuentan que los cuerpos se hallan inicialmente en reposo... pero ¿podrían estar moviéndose para cualquiera de los dos lados en cualquiera de los dos casos? |
|
 |
| |
| Algún derecho quedó sin reservar.
No se permite su reproducción sin citar la fuente. Ojito. Última actualización may-13. Buenos Aires, Argentina. |
|
|
|

