home  | más de dinámica | otros temas de Física | lecciones del maestro Ciruela | tonterías |  @ 
NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Leyes de Newton)

  

¡no me salen!

NMS 1.17- El sistema de dos bloques de la figura, cuyas masas son mA= 3 kg y mB= 2 kg respectivamente, se está moviendo hacia arriba.
Hallar qué aceleración tienen, y qué fuerza soporta la soga 2, cuando la soga 1 tira con la fuerza F, con las intensidades siguientes:

a- |F| = 80 N
b- |F| = 50 N
c- |F| = 30 N
d- |F| = 0

Este ejercicio es muy sencillo, y posee varias enseñanzas fundamentales. Trataré de destacarlas todas. Lo primero, como siempre son los DCLs.
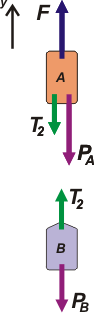diagrama de cuerpo libre - No me salen

Primero: nunca hay que olvidarse de consignar un Sistema de Referencia (SR). Fijate, en el esquema, es la flechita que apunta hacia arriba y que llamé y (el nombre es arbitrario).

Segundo: las sogas que utilizamos son sogas sin masa, eso asegura que las furzas ejercidas en ambos extremos son iguales. Eso me permitió hacer dos cosas: por un lado reemplacé la fuerza que hace la soga de arriba por F. Por otro lado las fuerzas que hace la soga 2 sobre ambos cuerpos le puse el mismo nombre, T2, ya que valen lo mismo.

Tercero: Los pesos de ambos cuerpos no tienen por qué ser iguales (en este caso no lo son), por lo tanto hay que individualizarlos, y los llamé PA y PB, respectivamente.

Una vez finalizados los DCLs, vienen las ecuaciones de Newton:

          ΣFA = mA a         →   F — T2 — PA = mA . a       [1]

          ΣFB = mB a         →   T2 — PB = mB . a              [2]
  Si vos sos de los que se resisten a utilizar subíndices... estás en la lona. Dedicate a otra cosa.

Cuarto: a las aceleraciones de los cuerpos no les puse subíndice, por el hecho de que nuestras sogas son inextensibles y eso asegura que las aceleraciones de ambos cuerpos sean iguales. A esa aceleración, a, solemos llamarla: la aceleración del sistema.

Ahora resolvemos el sistema de las dos ecuaciones y hallamos las incógnitas: si las sumamos miembro a miembro obtenemos...

F — PA — PB = (mA + mB) . a

Despejamos la aceleración, la calculamos:

    
a =   F — PA — PB  
mA + mB
   
Con ese valor vamos a cualquiera de las ecuaciones de Newton (acá lo hice en la [2]), depejamos T2 y la calculamos (a vos te conviene hacerlo en ambas y verificar que te da lo mismo):    
T2 =   PB + mB . (F — PA — PB)  
mA + mB
   
  a = 6 m/s²          T2 = 32 N caso a)
   

En los casos siguientes, sólo cambia el valor de F, el sistema sigue siendo el mismo, de modo que sólo hay que recalcular.

    
  a = 0 m/s²          T2 = 20 N caso b)
   
  a = — 4 m/s²          T2 = 12 N caso c)
   
  a = — 10 m/s²          T2 = 0 N caso d)
   

Quinto: En ninguno de los casos podés saber si el conjunto está subiendo o bajando. En los cuatro casos podría estar haciendo ambas cosas. El signo de la aceleración sólo te informa si acelera hacia arriba o hacia abajo. Pero bien podría estar acelerando hacia abajo y subiendo (en ese caso se está frenando), o acelerando hacia arriba y subiendo (en ese caso sube cada vez más rápido), o acelerando hacia abajo y bajando (cada vez más rápido), o acelerando hacia arriba y bajando (en ese caso se está frenando)... o incluso tener aceleración cero y en ese caso puede subir o bajar con velocidad constante e incluso, estar detenido).

    

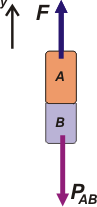Sexto: muchos estudiantes (a veces guiados por sus profesores) suelen simplificar los sistemas "uniendo" los cuerpos y considerando la masa del conjunto y el peso del conjunto.

La ecuación de Newton correspondiente quedaría así:

ΣFAB = mAB a         →   F — PAB = mAB . a

Es cierto, algo se simplifica. Y verás que los valores de aceleración dan igual que antes. El problema es que T2 queda oculta, ya que se transforma en una fuerza interna, y no tenés cómo calcularla. De todos modos no está mal, pero es mucho más aleccionador, hacer los diagramas de cada cuerpo por separado.
 

DESAFIO: Repasar las seis lecciones importantes de este ejercicio. Y encontrarle un sentido físico a cada uno de los resultados, tratando de predecirlos sin hacer cuentas (no es difícil).

  
Algunos reservados (no es que sean tímidos, callados). Se permite su reproducción citando la fuente; se puede prestar y/o regalar, se prescriben abrazos como recompensa. Última actualización jun-08. Buenos Aires, Argentina.