NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Leyes de Newton, estática)
|
|

|
 |
NMS 1.6- Si quisieras acostarte en una hamaca paraguaya
cuyas cuerdas de suspensión están desgastadas ¿qué es mejor, colgarla de dos árboles
cercanos o distantes? |
|
Pregunta fácil si la hay... si quisiera acostarme en una hamaca paraguaya es porque estoy cansado. Luego, me conviene atarla en árboles cercanos y no tener que caminar hasta árboles distantes, ¿hasta dónde quieren que vaya?... ¡Que estoy cansado! ¡No lo entienden!
Bueno, era una broma, no protestes, que este material es gratarola. Hablando en serio, este problema se puede resolver de varias maneras, algunas muy sencillas e ingeniosas. Pero yo lo voy a hacer del modo clásico. Empecemos con un esquema. |
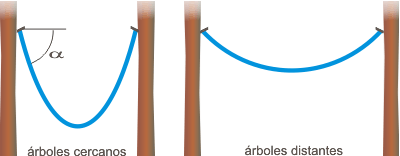 |
|
|
Supongo que los esquemitas te ayudan a entender el problema. El peso que va a soportar la hamaca en cualquier caso es el mismo: el tuyo. Pero parece que en un caso se puede romper más fácil, lo mismo que tu columna, y la diferencia pasa por el ángulo con que la hamaca queda amarrada al árbol, que en el esquema llamé α.
Cuanto más juntos estén los árboles mayor será α. Si los árboles estuviesen separados la distancia máxima (el largo de la hamaca) α valdría cero. ¿Vamos bien?
Para hacer las cosas más sencillas vamos a suponer que tu cuerpo es puntual (sin ánimo de ofenderte) con lo que la hamaca adquiere forma de "V" y vamos a tratar de expresar el problema en función del ángulo. No olvides que el largo de la hamaca es constante. |
|
|
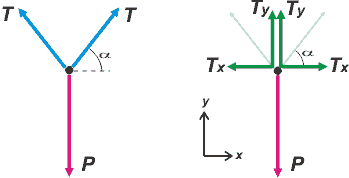 |
|
|
El de la izquierda es el DCL verdadero, como corresponde. P es tu peso, que está sostenido por las tensiones que hacen las dos mitades de la hamaca, que como toda hamaca paraguaya auténtica hace la misma fuerza en ambos extremos de modo que les puse el mismo nombre: T. El DCL de la derecha es el mismo pero ya descompuse las tensiones en dos direcciones x e y, que nos ayuda a plantear las ecuaciones de Newton. Tené en consideración algunas cositas:
Tx = T cos α
Ty = T sen α
ax = ay = 0 (se supone que no vas a hamacarte)
Entonces las ecuaciones de Newton quedan así:
en x → ΣFx = 0 → T cos α — T cos α = 0
Esta ecuación no dice nada interesante, pero la que sigue...
en y → ΣFy = 0 → 2 T sen α — P = 0
De esta última, podemos despejar T: |
|
|
| |
T = P / 2 sen α |
fórmula complementaria nro. 635* |
|
|
|
| Basta con que coloques dos valores diferentes para α y te das cuenta que cuanto más juntos estén los árboles menor es la tensión que debe soportar la hamaca. No deja de haber una situación de compromiso, ya que cuanto más juntos estén los árboles más incómodo es el descanso. Y cuanto más separados, aumenta el peligro de una rotura de hamaca. Demos la respuesta: |
|
|
Si quisiera acostarme en una hamaca paraguaya
cuyas cuerdas de suspensión están desgastadas es mejor colgarla de árboles
cercanos, aunque descanse incómodo, añamenhuí. |
|
|
DISCUSION: El resultado que te recuadré en verde tiene toda la descripción del problema: las unidades son correctas, pues las tensiones se deben medir en N, el peso es una fuerza también de modo que se mide en N, y el divisor son sólo números. Vamos bien. El peso es constante (a menos que adelgaces). Todo parece depender del sen α. Esta función varía de 0 a 1; cuando α vale 90º, sen α vale 1. Y cuando α vale 0º , sen α vale 0... y ya no se puede calcular la tensión porque está prohibido dividir por cero... pero lo peor es que nos damos cuenta que cuando α se va acercando a 0º la tensión crece infinitamente... o sea, es imposible subirnos a una hamaca sin que las cuerdas se inclinen un poco, o sin romperla. Y, saben, eso es justo lo que yo creía. |
|
|
| DESAFIO: ¿Para qué ángulo α la tensión de la hamaca es igual al peso? |
|
 |
| |
|
| *Anotate esta fórmula complenetaria en el machete. Las fórmulas complementarias constituyen un método sencillísimo para resolver ejercicios, y aseguran que jamás vas a aprender Física. Ja, ja, ja, jo, jo, ji, ji, ji... |
|
|
| |
|
| Algunos derechos reservados.
Algunos zurdos extrovertidos. Se permite su reproducción citando la fuente. Última actualización set-06. Buenos Aires, Argentina. |
|
|
|

