NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Movimiento oscilatorio armónico)
|
|

|
| |
FIS 102 (d6.07) - Una partícula oscila con un movimiento armónico simple de tal forma que su
desplazamiento varía de acuerdo con la expresión
x(t) = 5 cm cos (2 s-1 t + π/6),
donde x se mide en
cm y t en s. En t = 0 s, encontrar:
a) La posición.
b) La velocidad.
c) La aceleración.
d) El período y la amplitud del movimiento. |
OK, a no asustarse, es una papa. Funciona como cualquier ecuación horaria:
x(0s) = 5 cm cos (2 s-1 0 s + π/6)
x(0s) = 5 cm cos (π/6)
x(0s) = 5 cm 0,866
|
|
|
|
|
|
Para conocer la velocidad necesitamos la ecuación de la velocidad, pero antes necesitamos la amplitud (ω y φ ya los tenemos). Compará el modelo de ecuación horaria con el aportado por el enunciado:
x = A cos ( ω t + φ)
x = 5 cm cos (2 s-1 t + π/6)
No cabe duda de cuánto vale la amplitud: |
|
|
|
|
|
Ahora podemos armar la ecuación de velocidad:
v = − ω A sen ( ω t + φ)
v = − 2 s-1 5 cm sen ( 2 s-1 t + π/6)
Y le pedinos que hable del instante 0 s:
v(0s) = − 10 cm/s sen ( 2 s-1 0 s + π/6)
v(0s) = − 10 cm/s sen (π/6)
v(0s) = − 10 cm/s 0,5
|
|
|
|
|
|
Con la aceleración, ídem:
a = − ω² A cos ( ω t + φ)
a = − 4 s-2 5 cm/s cos ( 2 s-1 t + π/6)
a(0s) = − 20 cm/s2 cos ( 2 s-1 0 s + π/6)
|
|
|
|
|
|
Para conocer el período, τ, tenés que recordar su relación con la pulsación:
τ = 2 π / ω
τ = 2 π /2 s-1
|
|
|
| |
|
|
| Y van los gráficos. |
|
|
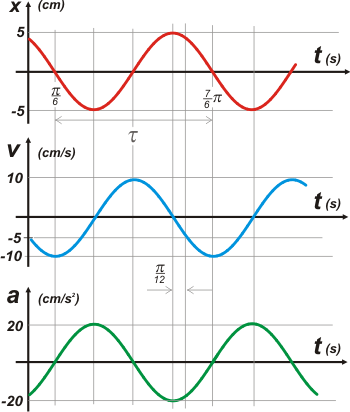 |
Como siempre en tándem (eso es innegociable)
Marqué algunos valores pero vos podés encontrar muchos más.
También podés apreciar cómo cada gráfico inferior describe la derivada del gráfico superior.
Y, sobre todo, podés disfrutarlos. |
|
|
|
| DESAFIO: La posición en el instante 4 s. |
|
 |
| |
| Algunos derechos reservados con anticipación.
Se permite su reproducción citando la fuente. Última actualización abr-16. Buenos Aires, Argentina. |
|
|
|

