NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(rozamiento y elásticas)
|
|

|
| |
|
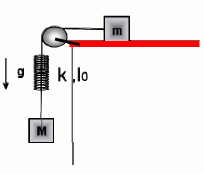
FIS 91 (d5.13) - Ídem ítems a) y b) del problema anterior, considerando la
configuración de la figura.
c) Considerar ahora que hay rozamiento entre m y el piso. Encontrar
el valor mínimo que debe tener el coeficiente de rozamiento estático,
μe, para que el sistema esté en equilibrio. Si el sistema se encuentra
en equilibrio, ¿cuánto vale la longitud del resorte?
|
 |
d5.12 -
a) Suponiendo rozamiento nulo entre el bloque y el piso. Calcular
la longitud del resorte cuando el sistema está en equilibrio. ¿Cuál
es la fuerza que ejerce el resorte sobre la pared en este caso?
b) Considerar ahora que el sistema no está en equilibrio. Si la
longitud del resorte es Lo y se deja el sistema en libertad, calcular
la aceleración inicial de cada bloque. |
|
|
Tampoco éste tiene mucho misterio. |
|
|
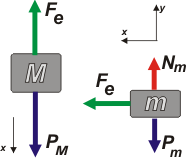 |
La cuerda intermedia la consideré como una prolongación del resorte (gracias por comprender).
Sin rozamiento este sistema no puede alcanzar nunca el equilibrio. Fijate, lo voy a plantear como si ese equilibrio existiese:
Fe = 0
Nm = Pm
PM = Fe
|
|
|
|
Si combinás las ecuaciones te das cuanta que el sistema sólo podría estar en equilibrio si la masa M fuese nula. |
|
|
| |
no es posible tal equilibrio |
respuesta a) |
|
|
|
Si lo analizás un poquito te das cuenta que al soltar los cuerpos con el resorte sin estirar (fuerza elástica nula), el curpo m no está solicitado por fuerza alguna, en cambio el cuerpo M lo está por la Tierra. |
|
|
| |
am = 0 , aM = g |
respuesta b) |
|
|
|
Claro, esa situación dura un instante (si la palabra dura fuese apropiada) pero al toque el resorte se estira y la situación cambia: la aceleración de M disminuye y la de m aumenta.
Vamos al ítem c). Todo en equilibrio (a = 0). |
|
|
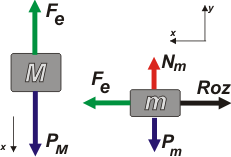 |
Fe = Roz
Nm = Pm
PM = Fe
Fe = k Δxc
Roz = μe Nm
|
|
|
|
Calculemos las cosas que nos piden:
μe = Roz / Nm
μe = Fe / Pm
μe = PM / Pm
Y por otro lado...
Δxc = Fe / k
Δxc = PM / k
|
|
|
| |
μe = M / m, L = Lo + M g / k |
respuesta c) |
|
|
|
| |
|
|
| DESAFIO: ¿Qué cambiaría si el resorte tuviera la misma constante elástica pero el doble de espiras? |
|
 |
| Algunos derechos reservados.
Se permite tu reproducción pero ahí no me cites. Última actualización abr-16. Buenos Aires, Argentina, América Latina, Planeta Tierra, Sistema Solar, Galaxia Via Láctea, Universo. |
|
|
|

