NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(rozamiento y elásticas)
|
|

|
| |
|
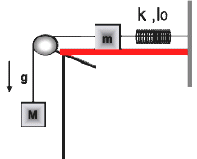
FIS 9 (d5.12) - Dos bloques de masas m y M están unidos por una cuerda ideal que
pasa por una polea ideal. El bloque de masa m está unido a la pared mediante un resorte ideal de
constante elástica k y largo natural Lo.
a) Suponiendo rozamiento nulo entre el bloque y el piso. Calcular
la longitud del resorte cuando el sistema está en equilibrio. ¿Cuál
es la fuerza que ejerce el resorte sobre la pared en este caso?
b) Considerar ahora que el sistema no está en equilibrio. Si la
longitud del resorte es Lo y se deja el sistema en libertad, calcular
la aceleración inicial de cada bloque.
|
 |
| c) Considerar ahora que el rozamiento entre bloque m y el piso no es despreciable. Si se desplaza al
cuerpo que cuelga hacia abajo hasta que el resorte tenga una longitud L y se lo suelta, encontrar el
valor mínimo que debe tener el coeficiente de rozamiento estático μe para que el sistema, al soltarlo,
quede en equilibrio. ¿Depende este valor de la constante elástica del resorte? |
|
|
Tanta ingeniería en un sistema tan complicado... para un ejercicio sencillísimo. |
|
|
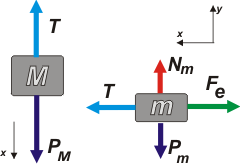 |
Como todo está en equilibro, o sea, no hay aceleración... Newton dice:
T = Fe
Nm = Pm
PM = T
Y además tenemos Hooke.
Fe = k Δx
|
|
|
|
Si unimos la primera con la tercera...
Fe = PM
Como el enunciado no ofrece datos numéricos, la respuesta es ésa: |
|
|
|
|
|
Como el resorte es un resorte ideal la fuerza que hace contra la pared es igual a la que hace contra en cuerpo de masa m (en este caso igual lo sería aunque el resorte no fuese ideal).
Su estiramiento valdría:
Δx = Fe / k
Y su longitud en esta situación:
La = Lo + Δxi
|
|
|
| |
La = Lo + M g / k |
respuesta a) |
|
|
|
En la situación b) el sistema no está en equilibrio ya que el resorte mide su propia longitud natural, de modo que no hace fuerza, Fe = 0. Ahora Newton dice:
T = m a
PM − T = M a
Como la soga es inextensible la aceleración de ambos cuerpos es idéntica (por eso no les puse subíndice). Combinando ambas ecuaciones: |
|
|
| |
a = M g / (M + m) |
respuesta b) |
|
|
|
En el ítem c) el sistema vuelve a estar en equilibrio pero gracias a la acción de una fuerza de rozamiento ya que la fuerza elástica tiene un valor diferente al del ítem a). Hagamos un nuevo DCL. |
|
|
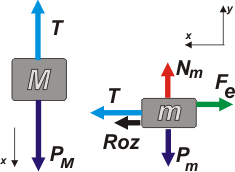 |
T + Roz = Fe
Nm = Pm
PM = T
Fe = k Δxc
Y agregamos:
Roz = μe Nm
|
|
|
|
Metemos todo en la licuadora algebraica...
Roz = μe Pm
PM + μe Pm = Fe
Despejamos μe, y ya. |
|
|
| |
μe = (k Δxc− M g) / m g |
respuesta c) |
|
|
|
En el caso planteado la longitud del resorte es la máxima posible sin que al soltarlo se rompa el equilibrio. Pero también hay otra longitud en que el equilibrio se mantiene gracias a que la fuerza de rozamiento es la estática máxima... ¿cuál es? |
|
|
| DESAFIO: ¿Qué cambiaría si el resorte tuviera la misma constante elástica pero la mitad de las espiras? |
|
 |
| Algunos derechos reservados.
Se permite tu reproducción pero ahí no me cites. Última actualización abr-16. Buenos Aires, Argentina, América Latina, Planeta Tierra, Sistema Solar, Galaxia Via Láctea, Universo. |
|
|
|

