 |
NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Fuerzas elásticas)
|
|

|
| |
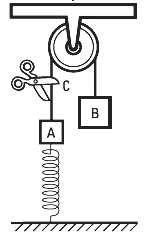
FIS 86 (d5.08)- En el sistema mostrado en la figura, un
extremo del resorte está unido al cuerpo A, y el
otro extremo al piso. Se pueden despreciar las
masas del resorte, de la cuerda y de la polea, así
como el rozamiento en la misma. Determinar la
intensidad de la fuerza que el resorte ejerce sobre
A, y la que soporta el techo,
para distintos valores de
las masas, en equilibrio.
Hallar también con qué
aceleración comenzará a
moverse el cuerpo A en cada
caso, un instante después
de cortar bruscamente
la cuerda en el punto C.
a- mA = 4 kg; mB = 6 kg
b- mA = 4 kg; mB = 1 kg
c- mA = mB.
|
 |
|
| Tenés que darte cuenta que te están preguntando por seis situaciones distintas. |
|
|
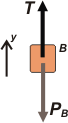 |
En la primera de todas, el resorte está estirado y está tirando de la masa A hacia abajo. Es fácil deducir eso por lo siguiente: Al estar el sistema en equilibrio (aceleración nula) la tensión de la soga es igual al peso de B. Eso podés verlo claramente en el DCL para el cuerpo B.
T — PBa = 0 → T = PBa
|
|
|
|
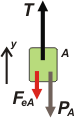 |
Sobre el cuerpo A actúan tres fuerzas... y la suma de ellas debe dar 0. Para poder ejercer esa fuerza, el elástico tiene que estar estirado.
T — PAa — Fea = 0
PBa— PAa — Fea = 0
Despejemos la fuerza elástica y la calculamos:
Fea = PBa — PAa = 60 N — 40 N
|
|
|
Situación a)
mAa = 4 kg
mBa = 6 kg |
|
|
|
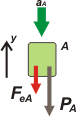 |
Acá viene la segunda situación. Si cortás la soga, la fuerza que ella hace, T, desaparece. El nuevo DCL aclara el asunto. Y las otras dos fuerzas no cambian. El peso no cambia porque es constante; y la fuerza elástica es la misma que antes porque nos están preguntando por el instante en que la cuerda se corta, de modo que el resorte todavía no tuvo tiempo de acortarse.
— PAa — Fea = mAa aAa |
|
|
|
|
|
|
| Ahora pasamos a la tercera situación en la que se cambian los cuerpos. |
|
|
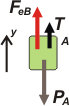 |
En este caso el elástico esta comprimido, no estirado como en el anterior. Los procedimientos son los mismos que antes:
PBb — PAb + Feb = 0
Despejemos la fuerza elástica y la calculamos:
Feb = PAb — PBb = 40 N — 10 N
|
|
|
Situación b)
mAa = 4 kg
mBa = 1 kg |
| |
|
|
| La cuarta situación es la que tiene la misma distribución de masa que la anterior, pero se corta la cuerda. |
|
|
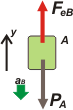 |
La fuerza elástica es, por supuesto, la que calculamos recién... entonces:
Feb — PAb = mAb aAb
|
|
|
|
| |
|
|
| En una quinta situación nos vuelven a cambiar las masas. Ahora ponen dos desconocidas pero iguales entre sí. Como consecuencia de esto, la soga realiza una fuerza igual al peso de A. Por lo tanto el elástico se queda sin nada que hacer. |
|
Situación c)
mAc = mBc |
|
|
 |
| |
| Por último, al desaparecer la tensión, el cuerpo A cae por su propio peso, y nada más. |
|
|
|
| También nos pedían la fuerza que hace el techo FT. No es difícil. Mirando la roldana (que no tiene masa) vemos que siempre es el doble de la tensión de la cuerda... o sea, el doble del peso de B. |
|
| |
FTa = 120 N; FTb = 20 N; FTc = 2 mBc g |
|
|
|
| Cuando la cuerda se corta el techo deja de hacer fuerza. |
|
| DESAFIO: ¿Qué resultados cambiarían si se reemplaza el resorte por otro de constante elástica doble? |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Cuando cuelgues algo del techo, procurá que no sea tu cuello. Última actualización jun-08. Buenos Aires, Argentina. |
|
|
|

