NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Fuerzas gravitatorias)
|
|

|
| |
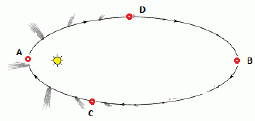
FIS 79 (d4.12) - La imagen representa la trayectoria elíptica del
cometa Halley en su movimiento alrededor del Sol (en
sentido horario).
a) Representar el vector fuerza sobre el cometa en las
posiciones A (perihelio), B (afelio), C y D.
|
 |
b) Representar las componentes tangencial y normal
(centrípeta) de la aceleración en dichos puntos. ¿Qué puede concluir acerca del módulo de la
velocidad del cometa en los puntos A y B?
c) En el punto A la distancia del cometa al Sol es 0,57 UA (1 UA = distancia Tierra-Sol) mientras
que en B es 35,5 UA. Si la masa del cometa es de 2,2 x 1014 kg; calcular la fuerza sobre el cometa y
su aceleración en dichos puntos.
d) Investigar en qué año se producirá la próxima aparición del Halley. Estimar sus probabilidades de estar vivo para verlo y si la resolución de este problema incrementará o no sus deseos de haceerlo. |
|
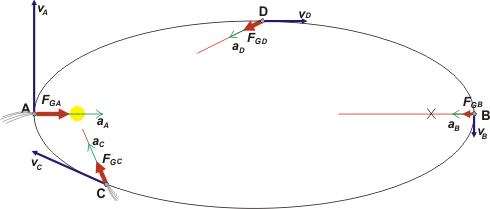
Bonito ejercicio, me da ganas de ser muy viejo para ver el Halley iluminando el cielo. Vamos a la representación gráfica. |
|
|
 |
|
|
Ahí tenés un esquema que muestra las velocidades tangenciales, las fuerzas gravitatorias y las aceleraciones. Las fuerzas gravitatorias siempre apuntan al Sol (tal como manda Newton), y las aceleraciones idem. Ya las vamos a calcular. El esquema no está en escala pero sirve para que te des una idea. No te olvides que la distancia al Sol en el perihelio, A, es 62 veces más chica que en el afelio, B.
Fijate que en todas las representaciones dibujé la aceleración proporcional a la fuerza (para no ofender a don Isaac).
Vamos a hacer una ampliación de cada momento indicado para evaluar correctamente las direcciones de la aceleración centrípeta y tangencial. |
|
|
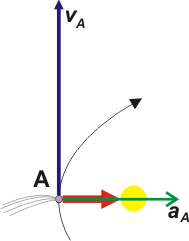 |
En el perihelio, A, la aceleración del cometa es totalmente centrípeta, no tiene componente tangencial. De hecho ahí el módulo de la velocidad tangencial del cometa deja de crecer y comienza a frenarse.
La cola del cometa (la cometa) son partículas de gas y polvo que se evaporan debido a la proximidad con el Sol y salen despedidas para todas partes. Pero el viento solar las echa para atrás como a una cabellera. La curvatura de la cola es simplemente la composición de los movimientos relativos de las partículas y del avance del cometa. El espectáculo es maravilloso. |
|
|
|
| Vamos a la posición D que es muy reveladora. |
|
|
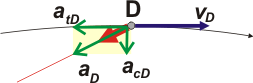 |
La aceleración, que apunta al Sol se descompone en una proyección tangencial a la trayectoria, atD, y otra normal, acD.
Esa aceleración tangencial (contraria a la velocidad, nos indica que el cometa se mueve cada vez más lento, Y así seguirá frenando hasta llegar al punto más alejado. |
|
|
|
| A esta distancia no hay cola, el cometa es una piedra berreta e invisible desde la Tierra. Vamos a ese punto más alejado. |
|
|
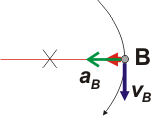 |
En el afelio, B, la aceleración vuelve a tener dirección normal a la trayectoria de modo que la aceleración tangencial se anula. Es en ese punto en el que deja de frenarse y empieza a ganar rapidez nuevamente.
La crucecita del gráfico te marca el segundo foco de la elipse (simétrica respecto de la posición del Sol, que ocupa el primer foco). |
|
|
|
| Finalmente, el punto de aproximación C, que es muy interesante. |
|
|
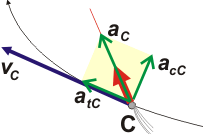 |
El cometa se aproxima al Sol y comienza a desplegar su cabellera. La aceleración, que siempre apunta hacia el Sol se descompone en una dirección paralela, atC, y otra perpendicular, acC,a la velocidad.
La aceleración tangencial que ahora tiene el mismo sentido que la velocidad nos revela que el cometa está ganando rapidez. |
|
|
|
Fijate que a la aceleración normal podemos llamarla centrípeta, pero no apunta hacia ningún centro de nada (¹). La elipce tiene un centro y dos focos, pero la aceleración centrípeta no apunta a ninguno de ellos salvo en cuatro instantes.
Vamos a los cálculos. La fuerza gravitatoria y la aceleración en A.
FGA = G . mH . MS / dA²
FGA = 6,67 10-¹¹ Nm2kg-2 2,2 x 1014 kg 2 x 1030 kg / (0,57 1,5 x 1011 m)²
FGA = 4 . 10¹² N
Divido eso por la masa del Halley y obtengo la aceleración:
aA = 4 . 10¹² N / 2,2 x 1014 kg
|
|
 |
| |
FGA = 4 . 10¹² N , aA = 1,82 x 10-2 m/s² |
|
|
|
|
Repito los cálculos para el punto B.
FGB = G . mH . MS / dB²
FGB = 6,67 10-¹¹ Nm2kg-2 2,2 x 1014 kg 2 x 1030 kg / (35,5 1,5 x 1011 m)²
|
|
|
| |
FGB = 1 . 109 N , aB = 4,7 x 10-6 m/s² |
|
|
|
|
La fuerza en B es unas 4.000 veces menor que en A. Pero no te preocupes, el Halley no se escapará y volverá a darse una vuelta por nuestro barrio.
(¹) Apunta hacia el centro de la circunferencia osculatriz. |
|
|
| |
|
|
| DESAFIO: Se llama excentricidad de una elipse a la posición de los focos en relación al radio mayor de la elipse. A los fines de la claridad en este ejercicio dibujé una elipse poco excéntrica (aproximadamente 0,8). ¿Pero cuánto vale la excentricidad de la órbita de Halley y cuánto la terrestre? |
|
 |
Algunos derechos reservados.
Se permite su reproducción citando la fuente. Agradezco a Fiama Picco por el envío de una errata. Última actualización abr-16. Buenos Aires, Argentina.
|
|
|

