NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Gravitación)
|
|

|
| |
FIS 76 (d4.09) - Un satélite artificial se dice que es geoestacionario si está siempre en la vertical de un cierto
punto de la Tierra. ¿A qué altura se encuentran los satélites geoestacionarios?
Radio y masa de la Tierra: RT = 6.360 km, MT = 6 . 1024 kg
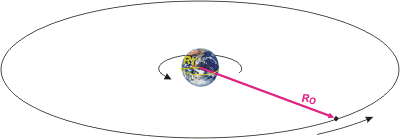
A ver, fijate si te cierra este esquemita. Ahí está nuestro hogar, y en el mismo plano del ecuador, pero mucho más lejos está orbitando un satélite que gira en el mismo sentido que la Tierra. Luego, si pegan una vuelta completa (período, τ) en el mismo tiempo, o sea en un día exacto, para ser más precisos en 24 horas, o mejor aún en 86.400 segundos, entonces se va a encontrar siempre arriba del mismo punto del ecuador (acordate que el ecuador es el plano perpendicular al eje de rotación de la Tierra que forma un círculo máximo, es el mayor de los paralelos).
A ese tipo de artefacto se lo llama satélite geoestacionario. Tenés uno y te llenás de guita; es como ser dueño de una antena de miles de kilómetros de altura. I-Sat -la empresa de televisión por satélite- usa una de esas, fijate, todas sus antenas parabólicas apuntan para ahí. |
 |
|
|
| RO es el radio de giro o radio de órbita del satélite. RT es el radio terrestre. La altura, h, a la que hay que ubicar el bicho es h = RO — RT. Si cazaste todo esto vamos bien. El DCL nos va a decir cuáles son las fuerzas que obran sobre el satélite. |
|
|
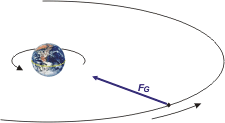 |
¡Una sóla! ¡La fuerza de atracción gravitatoria que le imprime la Tierra! ¡La soga invisible con que revolea al satélite haciéndolo girar a lo loco! ¡La cuerda intangible con que lo tiene atado y si lo soltara el satélite fugaría al infinito volando en línea recta y velocidad constante! La que Newton imaginó y cuantificó. |
|
|
|
Entonces:
FG = G . ms . MT / RO²
Pero además de estar sometido a esta fuerza, el satélite cumple con la 2da. ley de la dinámica, como cualquier objeto hijo de vecino. De modo que:
ΣF = m . a
donde la sumatoria de fuerzas, ΣF, es FG, y a es de tipo centrípeta , entonces...
FG = ms . 4π² . RO / τ²
Juntando las dos ecuaciones tenemos:
G . ms . MT / RO² = ms 4π² . RO / τ²
Cancelamos la masa del satélite (parece que cualquier artefacto que pongamos se va a comportar igual), reagrupamos...
RO³ = τ² . G MT / 4π²
RO = (τ² . G MT / 4π²) 1/3
RO = 42 x 106 m
Como h = RO — RT |
|
exponente 1/3 es lo mismo que raíz cúbica |
| |
h = 36.000 km |
3 Tierras de distancia, un pedazo |
|
|
35.786 km, para ser más precisos |
| |
|
|
DISCUSION: La expresión RO³ = τ² . G MT / 4π² es válida para cualquier objeto satélite natural o artificial de otro objeto, como estrellas o planetas. Una forma muy parecida de esta expresión, que muestra la proporcionalidad entre los cubos de los radios de órbita y los cuadrados de los períodos se denomina Tercera Ley de Kepler, en honor al loco obsesivo que, gracias a su locura y obsesión, la descubrió antes de que pudiese existir una explicación. La explicación la encontró Don Isaac Newton unos 50 años después. Curiosidades de la ciencia.
Chivo: ¿querés conocer más sobre satélites y en especial sobre los satélites argentinos? Te recomiendo mi libro: Satélites, de la Luna al Arsat. |
|
 |
| DESAFIO: Explicar en no más de 25 palabras por qué los satélites como éstos (geoestacionarios) sólo pueden orbitar en el plano ecuatorial... y te la tenés que comer. |
|
| Algunos derechos reservados.
Se permite su reproducción chapoteando en la fuente (aunque quede borroneada). Última actualización oct-06. Buenos Aires, Argentina. |
|
|
|

