 |
NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Leyes de Newton, dinámica del movimiento circular) |
|
|

|
| |
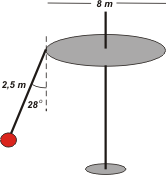
FIS 64 (d3.17) - Un juego de un parque de atracciones consta de una plataforma
circular de 8 m de diámetro que gira. De la plataforma cuelgan “sillas
voladoras” suspendidas de cadenas de 2,5 m de longitud. Cuando la
plataforma gira, las cadenas que sostienen los asientos forman un
ángulo de 28º con la vertical.
a) ¿Cuál es la velocidad angular de las sillas?
b) Si un niño ocupa una silla y la masa del conjunto silla-niño es de 50 kg, ¿cuál es la tensión que
ejerce la cadena?
|
 |
|
|
|
|
Uh... qué plomazo... esto ya lo hiciste78 veces. Es un péndulo cónico, ni más ni menos... si querés lo podemos llamar péndulo cónico truncado (porque le falta la punta), pero hasta ahí me estiro, ni un cachito más.
Aparentemente lo único que trae esto de novedad es un poco de complejidad geométrica, nada que te quite el sueño. A ver si estamos de acuerdo: el radio de giro de los chicos será: el apartamiento de la vertical (L sen 28°) más el radio de la plataforma, 4 m. Eso nos da: R = 5,17 m. Eso era todo, el resto: historia conocida. |
|
|
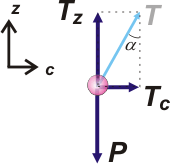
Son dos fuerzas solas para cada chico: su peso, P, y la fuerza que hacen las sogas, T.
Tc = T sen 28°
Tz = T cos 28°
Newton dice:
Tc = m . ω² . R
Tz = P
|
 |
|
|
|
Metemos todo en la licuadora algebraica...
T sen 28° = m . ω² . R
T cos 28° = m g
Dividimos miembro a miembro:
tg 28° = ω² . R / g
Despejamos y lo calculamos:
ω² = g tg 28° / R
ω² = 10 m/s² tg 28° / 5,17 m
|
|
|
|
|
|
La tensión de las cadenas te la cuenta directamente la ecuación en z.
T cos 28° = m g
T = m g / cos 28°
T = 50 kg . 10 m/s² / cos 28°
|
|
|
|
|
|
|
|
|
| DESAFIO: Nada de lo expuesto cambiaría si en lugar de colgar de una plataforma las sillas colgaran de un punto fijo como en un péndulo cónico, ¿para qué lo construyen con esa plataforma elevada? |
|
 |
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización abr-16. Buenos Aires, Argentina. |
|
|
|

