 |
NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Leyes de Newton, dinámica del movimiento circular) |
|
|

|
| |
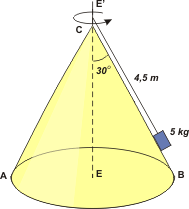
FIS 62 (d3.16) - Un cuerpo de 5 kg, apoyado sobre la superficie cónica ABC,
pende de una soga ideal de 4,5 m de longitud (ver figura). El cuerpo gira
alrededor del eje EE' a 10 rpm. No hay rozamiento entre la superficie y
el cuerpo. Calcular:
a) La fuerza que ejerce la superficie cónica sobre el cuerpo.
b) La tensión en la soga.
c) La velocidad angular a la que ha de girar el cuerpo para anular la fuerza
de contacto con la superficie cónica. ¿Cuánto vale la tensión de la soga en
este caso? Comparar éstos resultados con los del ejercicio DC-12.
d) Describir qué sucedería si el cuerpo girase con una velocidad angular
mayor que la calculada en c) ¿Y si lo hiciera con una velocidad angular
menor?
|
 |
|
|
|
|
| Si ya estuviste 2 horas quemándote las pestañas con este ejercicio, es momento de acordar conmigo que la parte fundamental de todo ejercicio de dinámica es el diagrama de cuerpo libre. |
|
|
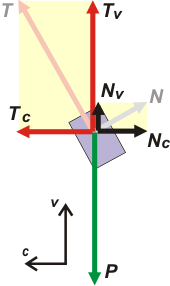
Las fuerzas que actúan sobre el cuerpo son 3: el apoyo, N, que es normal a la superficie del cono; la tensión que hace el piolín, T; y el propio peso del cuerpo, P.
En todos los ejercicio de movimiento circular es indicado utilizar uns sistema de referencia cuyos ejes apunten en la dirección centrípeta y vertical. Tené en cuenta que el centro de la circunferencia que describe el cuerpo no está en E ni en E'... está en un punto del eje EE'a la misma altura que se halla el cuerpo.
Las fuerzas T y N tuve que descomponerlas en esas direcciones. Y quedan así:
Tc = T sen 30°
Tv = T cos 30°
|
 |
|
|
|
Nc = N cos 30°
Nv = N sen 30°
Y las ecuaciones de Newton quedan así (ojo que N tira para afuera):
Tc − Nc = m aC
Tv + Nv − P = 0
Y listo... ya paso lo más difícil, te diría lo único difícil. El resto es álgebra de la escuela primaria: en las de Newton reemplazo las anteriores cuatro.
T sen 30° − N cos 30° = m 4 π² f² . R
T cos 30° + N sen 30° = P
Las únicas incógnitas son T y N, de modo que tirá la monedita, despejá una cualquiera, y lo que te da lo metés en la otra.
Tené en cuenta que f = 10 rpm = 0,167 s-1, y que R = L sen 30° = 2,25 m |
|
ac = ω² . R
= v² / R
= ω . v
= 4𲃲. R
= 4π²R / T²
= 2π v / T
= 2π v ƒ |
|
|
|
|
La velocidad angular necesaria para que el cuerpo justo se despegue de la superficie, nos remite al péndulo cónico simple y sencillo. Aunque no estaría nada mal que repitas todo este ejercicio pero teniendo en cuenta que ahora N = 0
|
|
|
|
|
|
| |
|
|
Si el cuerpo girase a una velocidad mayor que la anterior se despegaría de la superficie e imagínaría que está volando (¿tienen tanta imaginación los cuerpos?).
Y si girara a una velocidad menor, nada, giraría a una velocidad menor... y se aburriría. |
|
|
| |
|
 |
| |
|
| DESAFIO: ¿Debe tratarse de un MCU (velocidad angular constante)? |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización abr-16. Buenos Aires, Argentina. |
|
|
|

