 |
NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Leyes de Newton, dinámica del movimiento circular, péndulo cónico)
|
|

|
| |
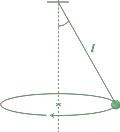
| FIS 61 (d3.14) - Una partícula de masa m, atada a una cuerda ideal de 4,5 m de longitud,
gira de modo que la cuerda forma un ángulo de θ con la vertical (péndulo cónico),
como muestra la figura. Despreciando todo clase de rozamiento, |
a) ¿Qué tipo de movimiento realiza la partícula?
b) Si θ = 30º, ¿cuánto vale la velocidad angular de la partícula? ¿Depende este
valor de su masa?
c) Si m = 5 kg, calcular la tensión que ejerce la cuerda.
d) ¿Cómo variarían el ángulo θ y la tensión de la cuerda si la partícula girara
con una velocidad angular mayor que la calculada en b)?
e) La partícula, ¿podría permanecer girando con la cuerda horizontal? Justifique. |
 |
|
Tal como indica el enunciado, se trata de un péndulo cónico. La partícula se mueve en una circunferencia con MCU, rapidez constante. Al girar el hilo describe un cono y de ahí el nombre del sistema. |
|
|
 |
Como todo ejercicio de dinámica... ya sabés por dónde hay que empezar.
Acá está el DCL, describiendo las dos únicas fuerzas que actúan sobre el péndulo cuando se halla en la misma posición que te lo dibujé en el esquemita. La fuerzas son; el peso de la masa, P; y la tensión con que lo tira la cuerda, T. |
|
|
|
| Hagamos algunas aclaraciones sobre el esquema del péndulo que me parece que son pertinentes y que después vamos a necesitar. |
|
|
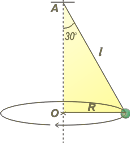 |
Cosas destacables del esquema. La circunferencia que describe el péndulo es horizontal y tiene su centro en O (¡no en A!), y su radio, R.
Calculemos el radio que seguro que lo vamos a necesitar:
R = l sen 30°
R = 4,5 m . 0,5
R = 2,25 m
|
|
|
|
| Bueno, tenemos que escribir las ecuaciones de Newton, pero, como las fuerzas no son co-direccionales, debemos descomponer una de ellas. Lo más práctico es descomponer T. Acá va el nuevo DCL. |
|
|
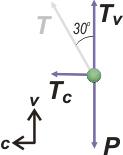 |
Recordás que siempre que enfrentás un MCU a uno de los ejes lo llamás c (por centrípeto), en lugar de x, ¿no? Es cierto que se trata de un eje que va cambiando con el tiempo. Pero no te olvides que la dinámica son sólo instantáneas del universo. Fijate que α = 30º (dos paralelas cortadas por una transversal generan ángulos alternos internos que son iguales entre sí, jijiji...) y eso permite establecer que:
TV = T . cos 30°
Tc = T . sen 30° |
|
|
|
Ahora sí, vamos a Newton. En el eje vertical tenemos que la aceleración es cero (la circunferencia de la trayectoria no cambia de altura, está quieta).
ΣFv = 0 → TV — P = 0 → TV = m . g [1]
ΣFc = m ac → Tc = m ac → Tc = m ω² R [2]
El resto es una pavada: en las ecuación [1] y [2] reemplazás las anteriores:
T . sen 30° = m ω² R
T . cos 30° = m . g
Si dividís miembro a miembro:
tg 30° = ω² R / g
Despejamos v y la calculamos:
ω² = g tg 30° / R
ω² = 10 m/s² 0,577 / 2,25 m
|
|
 |
|
|
|
Para calcular la tensión de la cuerda nos basta la ecuación de Newton dirección vertical:
T . cos 30° = m . g
T = m . g / cos 30°
T = 5 kg . 10 m/s² / 0,866
|
|
|
|
|
|
| Vamos con las últimas preguntas. Si la velocidad angular aumenta aumenta también el ángulo de separación con la vertical, aumenta el radio de giro, aumenta la fuerza que tiene que hacer el piolín... y varias otras cosas más. Pero por más que aumente la velocidad angular y la fuerza del hilo, nunca va a colocarse en posición horizontal... θ nunca puede alcanzar los 90º ya que la tensión siempre debe tener una componente vertical hacia arriba para compensar el peso. |
|
|
| |
|
|
|
|
 |
| DESAFIO: ¿Cuál es el error más frecuente en la resolución de los ejercicios de péndulo?l |
|
| Algunos derechos, zurdos y ambidiestros reservados.
Se permite su reproducción citando la fuente. Última actualización abr-16. Buenos Aires, Argentina. |
|
|
|

