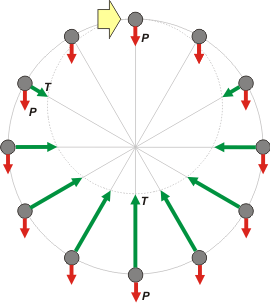
Este ejercicio también tiene una parte muy intuitiva. Vamos a aprovecharnos de eso: está claro, como en el ejercicio anterior, que cuanto más rápido gire la bola más tensa deberá estar la cuerda (aunque en este caso no se trate de una tensión constante). En las partes de abajo de la circunferencia el peso de la bola contribuye a que la tensión de la cuerda sea mayor. Y recíprocamente, en los recorridos por arriba de la trayectoria la fuerza peso hace que la tensión de la cuerda sea menos.

El mínimo de la tensión se hallará justo en la posición más alta, cuando la cuerda está en posición vertical; es ahí donde la tensión puede llegar a ser nula, aflojarse y hacer que la bola deje de describir una circunferencia. Tenemos una situación límite: la velocidad mínima en ese punto coincide con el valor nulo de la tensión, T = 0.

Está claro que no se trata de una velocidad constante. No se trata de un movimiento circular uniforme, la velocidad es mayor abajo que arriba. pero se trata de un análisis hecho en el instante en que la bola  pasa por la posición más alta.

No olvides que la dinámica no describe procesos (como la cinemática) son fotos instantáneas del universo.