| |
NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
Rozamiento |
|
|

|
| |
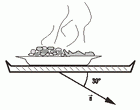
FIS d2.45 - Un plato cuya masa es m, viaja sobre la
bandeja del mozo del bar. Hallar el coeficiente de
rozamiento necesario entre el plato y la bandeja
para que no se deslice, cuando la bandeja se acelera
a 2 m/s² en la dirección indicada, manteniéndose
horizontal. |
 |
|
| Bonito problema si los hay. Como siempre debemos empezar por un DCL. ¿Probaste vos el tuyo? Esta es la mejor oportunidad para que te convenzas: TODO EL ESFUERZO EN DINAMICA TENES QUE PONERLO EN EL DCL... si lo hacés bien, el resto es una papa. Si lo haces mal... nada te salva. Bueno acá va. |
|
|
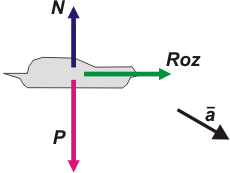 |
Había varias cosas de qué darse cuenta. Una era que el DCL que había que hacer era el del plato. Otra que la fuerza de rozamiento apuntaba a la derecha. La mayoría mete la pata y lo pone apuntando a la izquierda. Pero no es culpa de ellos, es que vienen escuchando una y mil veces ese error tan espantoso que suelen repetir hasta el cansancio los profesores de física: "la fuerza de rozamiento siempre es contraria al desplazamiento", y bueno tanto escucharlo, y a veces leerlo, se lo creen. Es una patraña. |
|
|
|
¿Cómo sigue la historia? Como siempre, después del DCL vienen las ecuaciones de Newton. Ojo, no te olvides que acá vas a tener que descomponer la aceleración en dos direcciones. Más vale descomponer un solo vector (la aceleración) y no tres (las tres fuerzas). |
|
|
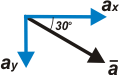 |
donde
ax = a cos 30º
ay = a sen 30º
|
|
|
|
ΣFx = m ax ⇒ Roz = m a cos 30º
|
|
|
ΣFy = m ay ⇒ N — P = — m a sen 30º
|
|
|
| No olvidemos lo que sabemos de las fuerzas de rozamiento, que en este caso es estático, ya que no queremos que el plato deslice de la bandeja, y además queremos que sea el estático máximo, así voy a poder mover la bandeja con más aceleración. |
|
|
Roz = μe . N
|
|
|
| Y lo que sabemos del peso. |
|
|
P = m . g
|
| |
| Metemos todo esto en las ecuaciones de Newton que quedan así: |
|
|
μe . N = m a cos 30º
N — m g = — m a sen 30º
Despejo μe de la primera y reemplazo N con lo que obtengo de la segunda |
|
|
| μe = |
|
m a cos 30º |
|
|
| m g — m a sen 30º |
|
|
|
| Veo que no importa la masa del plato ni si hay ravioles o churrascos. |
|
|
| μe = |
|
a cos 30º |
|
|
| g — a sen 30º |
|
|
|
|
|
|
| DISCUSION: Para discutir el resultado es mejor verlo así: |
|
|
|
|
|
Queda claro que las unidades son correctas, y qué pasaría si variáramos α.
Si α = 90º el μe necesario se hace cero, lógicamente, no hace falta fuerza de rozamiento lateral para subir o bajar la bandeja verticalmente. Y si α = 0º, entonces μe vale a/g, que es un resultado que ya obtuvimos antes. Por último, si la aceleración en lugar de ir hacia abajo fuera hacia arriba... qué cambiaría... Pues fíjate, el signo del denominador, en lugar de ser menos es más. O sea el denominador aumenta, por lo tanto el cociente, μe , disminuye. Muy razonable, ya que al acelerar para arriba tiene que hacerse mayor la normal, con lo que aumenta el agarre entre la bandeja y el plato. Me cierra perfecto, puedo laburar de mozo. |
|
|
| DESAFIO: First Encontrar tres explicaciones diferentes para convencer a un compañero que insiste en que la fuerza de rozamiento va para el otro lado. Second: resolver este mismo problema con un SR paralelo y perpendicular a la aceleración (en lugar de descomponer la aceleración vas a tener que descomponer las tres fuerza). No le tengas miedo, es una práctica muy buena. El resultado necesariamente es el mismo. |
|
 |
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Está absolutamente prohibido utilizar este material sin antes haber hecho un intento por resolver es problema sin ayuda. Severas penalizaciones a los infractores. Última actualización set-06. Buenos Aires, Argentina. |
|
|
|

