| |
NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
Rozamiento |
|
|

|
| |
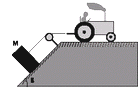
d2.43 - Un tractor puede subir o bajar un bloque
como indica la figura. ¿Cuál es la fuerza máxima
y mínima que puede hacer el tractor sin que la
caja deslice sobre el plano?
|
ß = 30°
µe = 0,5
µd = 0,4
|
 |
|
|
| Este ejercicio es muy interesante por varias razones, ya vas a ver. Pero una de ellas es que contiene una trampa cazabobos. Una trampa tan pero tan remanida, repetida, conocida y cocinada, que solamente cae el 57,4 % de los estudiantes que lo tratan de resolver. Vamos a los DCL y los comentamos. |
|
 |
|
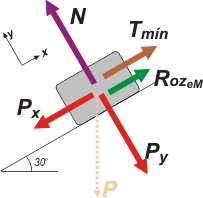
Te tengo que avisar un par de cosas de estos dos DCLs. Primero que tienen ya un grado de elaboración. Por ejemplo, sobre la caja actua su fuerza peso y no la dibujé (en realidad dibujé su huella en línea punteada), pero puse sus componentes según el SR que elegí (y que, como ya te habrás dado cuenta NUNCA ME OLVIDO DE INDICARLO).
Lo segundo es que son dos DCLs diferentes, porque describen situaciones diferentes. En el caso de arriba el tractor hace una fuerza pequeña, Tmin, que sería insuficiente para sostener quieta la caja. Sin embargo la caja no desliza. Debemos suponer que el rozamiento acude en su auxilio. Si esa fuerza Tmin es realmente la mínima, entonces coincide con que la de rozamiento es la máxima, RozeM.
En el segundo caso el tractor realiza una fuerza grande, superior a la necesaria para sostener la caja, pero aún así la caja no sube. ¿Qué estará pasando? No cabe duda de que el motivo es que la caja está trabada por el rozamiento. Si la fuerza de tractor es la máxima, antes de ponerla en movimiento efectivamente, Tmáx , será porque se le opone la fuerza de rozamiento máxima, nuevamente RozeM, pero ahora en sentido opuesto.
 |
| Primer DCL. Describe la situación en la que el tractor hace una fuerza pequeña como para sostener la caja. Aún así la caja no desliza hacia abajo, se ve que está algo trabada en el piso: es la fuerza de rozamiento estático que también tira hacia arriba. |
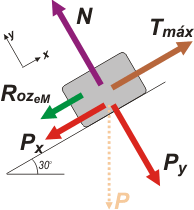 |
| Segundo DCL. Describe la situación en la que el tractor hace una fuerza superior a la necesaria para sostener la caja. Aún así la caja no asciende... se ve que está algo trabada en el piso: es la fuerza de rozamiento estática que tira de la caja hacia abajo. |
|
|
Me vas a preguntar para qué nos dan el μd, y yo te voy a contestar que efectivamente no sirve para nada excepto para cazar bobos. Pero para hacer honor a la verdad y al autor del problema te voy a agregar que me parece un agregado correcto, ilustre, didáctico. De hecho cuando el universo enfrenta a los científicos con preguntas, intrigas o problemas, no le muestra solamente los datos que va a necesitar para resolverlo. El universo muestra el universo y tiende trampas cazabobos y también cazagenios, ojalá caigas en una.
Bueno basta de cháchara, vamos a resolver el ejercicio. Después de todo DCL viene un set de ecuaciones de Newton, acá están. Ojo que sin que deslice significa a = 0.
caso 1, eje x → Tmin + RozeM — Px = 0
caso 2, eje x → Tmáx — RozeM — Px = 0
casos 1 y 2, eje y → N — Py = 0
Y además tenemos que
Px = P . sen 30º
Py = P . cos 30º
RozeM = μe . N
¿Necesitás algo más? No, metés todo eso en la licuadora algebraica y salen los valores que estás buscando. No llores, yo te lo hago. Pero intentalo sin ayuda antes.
Tmin = — μe . P . cos 30º + P . sen 30º
|
|
|
|
Tmáx = μe . P . cos 30º + P . sen 30º
|
|
|
|
| Estas respuestas nos indican que las fuerzas que hace el tractor (tanto la máxima como la mínima) dependen del peso de la caja. |
|
| |
| DESAFIO: ¿Cuáles serán las fuerzas necesarias para subir o bajar la caja con velocidad constante ? |
|
 |
| |
| Algunos derechos reservados.
Se permite reproducir este material sin lastimarlo y citando la fuente. Última actualización dic-06. Buenos Aires, Argentina. |
|
|
|

