| |
NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
Rozamiento |
|
|

|
| |
d2.38 - Entre los bloques A y B de la figura hay rozamiento,
así como también entre el bloque A y el
piso. En ambos casos el coeficiente de rozamiento
estático es 0,4 y el coeficiente dinámico es 0,2.
Si el conjunto de bloques se mueve hacia la
derecha, calcular el mínimo valor que debe tener
F para que el bloque B no caiga.
Datos: mA = 5 kg y mB = 1 kg
|
 |
| Te recomiendo resolver primero este ejercicio cuya única diferencia es que no tiene rozamiento entre el cuerpo A y el piso. |
|
Este ejercicio es una joyita. Felicito a su autor, que desconozco quién es, pero goza de mi admiración. Toda la dificultad reside en comprender el funcionamiento del sistema, ya que -superado ese escollo- es resto es fácil. Por otro lado, la originalidad es notable. Posee la virtud de estimular la comprensión física de los sistemas físicos y evitar la utilización de fórmulas en forma mecánica y sin comprender lo que está ocurriendo.
|
 |
Pero supongamos que no somos lo suficientemente clevers como para cazarlo al vuelo y demostremos -una vez más- que las herramientas dinámicas que yo te enseño son suficientemente poderosas como para hacer que lo resuelvas sin tropiezos. Vamos con los DCLs.
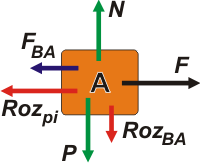
El diagrama de fuerza sobre el cuerpo A no presenta demasiadas dificultades. Las fuerzas que actúan sobre él son cinco:
Su propio peso, PA; el apoyo sobre el piso, N; la fuerza externa que es dato del enunciado, F; el rozamiento con el piso, Rozpi, la fuerza de rozamiento entre los bloques, RozBA, y la fuerza de contacto con el bloque B, FBA, que es la clave del ejercicio, ya verás. |
|
|
|
Quizás te cueste entender la presencia de la fuerza de rozamiento hacia abajo, RozBA, se trata del par de acción y reacción de la fuerza de rozamiento que sostiene al cuerpo B, y que discutiremos el el DCL que sigue.
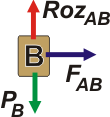
Sobre el cuerpo B actúan tres fuerzas. Obviamente su propio peso, PB. La fuerza de contacto con el cuerpo A, FAB. Y la fuerza de rozamiento que sostiene al cuerpo, RozAB. |
|
|
 |
Discutamos estas dos últimas un poco. Por un lado deberás admitir que la única fuerza capaz de sostener el cuerpo y evitar que el peso se lo lleve para abajo ("caiga por acción de la gravedad", como lo dice el enunciado) es la fuerza de rozamiento.
Por otro lado, deberás admitir que esa fuerza es de tipo estática (si fuese dinámica el cuerpo estaría deslizando hacia abajo y no sería la que buscamos.
Y por último, si estamos buscando un valor mínimo, debe tratarse de la fuerza de rozamiento estática máxima. |
|
|
|
Ahora, recordarás que la fuerza de rozamiento estática máxima es igual al coeficiente de rozamiento estático por la normal (RozeM = μe . N, es lo que figura en todos los libros). Pero ¿a qué se refieren con normal? Se trata de la fuerza de contacto entre las superficies en rozamiento, la fuerza que comprime las superficies en rozamiento... que en nuestro caso es... ¡FAB!
Vamos a las ecuaciones. Con el cuerpo A no hay mucho problema: |
|
|
F — FBA — Rozpi = mA . a |
[1] |
|
N — PA — RozAB = 0
|
[2] |
|
|
|
FAB y FBA,
como su nombre lo indica, son un par de acción y reacción, por lo tanto valen lo mismo. |
| Con el cuerpo B tampoco (toda la dificultad la superamos al hacer los DCLs). |
|
FAB = mB . a |
[3] |
|
RozAB — PB = 0
|
[4] |
|
|
|
| Por último los rozamientos: |
|
RozAB = μe . FAB
|
[5] |
|
Rozpi = μd . N |
[6] |
|
|
|
Ahora un poquito de álgebra. De la [3] despejo la aceleración y eso lo meto en la [1]:
F — FBA — Rozpi = FAB . mA / mB
De acá despejo F:
F = FBA + μd . N + mA . FAB / mB
F = FBA + μd . (PA + RozAB) + mA . FAB / mB
F = FBA + μd . PA + μd RozAB + mA . FAB / mB
F = FBA + μd . PA + μd μe FAB + mA . FAB / mB
F = FBA ( 1 + μd μe + mA/mB) + μd . mA g
Guardo eso para después. Antes igualamos la [4] con la [5] y despejamos FAB...
PB = μe . FAB
FAB = PB / μe
Y eso lo metemos en la que dejé esperando:
F = (PB / μe) ( 1 + μd μe + mA/mB) + μd . PA
F = (10 N / 0,4) ( 1 + 0,2 . 0,4 + 5) + 0,2 . 50 N
|
|
|
|
|
|
El ejercicio permite desestructurar creencias erróneas y adentrarse de lleno en la naturaleza de la fuerza de rozamiento: la fuerza que crea al rozamiento es la que comprime las superficies que rozan, es cierto que es normal (perpendicular) a las superficies en contacto, pero es más ilustrativo llamar a las fuezas por su naturaleza que por una propiedad geométrica. |
|
|
| DESAFIO: ¿Cuánto debería valer la aceleración del conjunto si se quiere que el bloque B no deslice y el coeficiente estático valiera 0,2? ¿Podría valer lo mismo e coeficiente estático que el dinámico? |
|
 |
| Algunos derechos reservados.
Se permite tu reproducción recitando en la fuente. Agradezco la lectura atenta de Carmen Lambrecht que detectó un error importante. Última actualización jul-11. Buenos Aires, Argentina. |
|
|
|

