| |
NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
Rozamiento |
|
|

|
| |
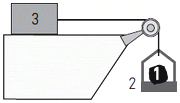
d2.35 - El cuerpo 1 de masa m1 = 10 kg está dentro
de una caja 2 de masa m2 = 30 kg. El conjunto está
atado a un tercer cuerpo de masa m3 = 100 kg mediante una soga y una polea ideal.
Se deja al sistema en libertad, desde el reposo,
y se observa que los cuerpos se desplazan 10 m durante los primeros 4 s. Calcular:
|
 |
a) La aceleración del sistema y el coeficiente
de rozamiento dinámico entre el cuerpo 3 y la
superficie horizontal.
b) La tensión de la cuerda.
c) La intensidad de la fuerza que el cuerpo 2
hace sobre el cuerpo 1. |
|
| |
|
|
Si en un examen de dinámica el tema pide que hagas el diagrama de cuerpo libre, no te olvides de hacerlo. Si no te lo pide... ¡tenés que hacerlo igual! Si no lo hacés, no solamente no vas a poder resolver el ejercicio, sino que tu lector/corrector/profesor no va a saber de qué estás hablando. Él no lee tu mente. |
|
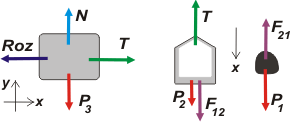 |
T − Roz = m3 a
N − P3 = 0
Roz = μd . N
F12 + P2 − T = m2 a
P1 − F21 = m1 a
|
|
|
|
Donde la aceleración, la misma para los 3 cuerpos, la calculás expeditivamente como lo hacés en cualquier MRUV. En este caso
a = 2Δx/Δt²
no necesito explicarte por qué. |
|
|
| |
|
|
El resto del álgebra es muy sencilla. La segunda en la tercera y a tercera en la primera:
T = m3 a + μd P3
Y la dejás esperando. Ahora despejás la fuerza de contacto de la última y lo metés en la anteúltima:
T = P1 + P2 − m1 a − m2 a
Y juntás estas dos:
m3 a + μd P3 = P1 + P2 − m1 a − m2 a
Despejás y lo calculás.
μd = (P1 + P2 − m1 a − m2 a − m3 a) / P3
|
|
|
|
|
|
| Con estos dos vas donde quieras, pero calculás el resto. |
|
|
|
|
|
| Ponele. |
|
|
| DESAFIO: ¿Podría el sistema moverse en sentido opuesto al mostrado en este ejercicio? En ese caso, ¿qué cambiaría? |
|
 |
| Algunos derechos reservados, otros no.
Se permite su reproducción citando la fuente. Última actualización mar-16. Buenos Aires, Argentina. |
|
|
|

