NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Leyes de Newton)
|
|

|
| |
 |
FIS d1.04 - Un cuerpo oscila dentro de una palangana
como indica la figura.
Dibuje la fuerza resultante que actúa en los
puntos A, B, C, D y E en un camino de ida y en un
camino de vuelta (se desprecia el rozamiento). |
|

|
|
Ok, yo lo hago... pero te advierto una cosa: no vas a poder sacarle todo el provecho que tiene si antes no estudiaste a fondo la dinámica de los movimientos circulares... la fuerza centrípeta y todo eso. Te propongo que si no lo hiciste, lo dejes para después. Te prometo que va a seguir estando.
En lugar de responder directamente el requerimiento del enunciado, voy a realizar un trabajo más pautado y -espero- aleccionador. Voy a empezar por representar todas las fuerzas que están actuando en cada posición. Acá va: |
|
|
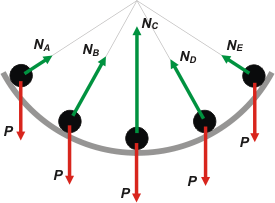 |
El cuerpo (que yo imaginé como una bolita negra) recibe en cada caso dos fuerzas solas, siempre las mismas.
Una de ellas es la fuerza peso, P. Se trata de una fuerza constante que siempre es vertical y siempre vale lo mismo para ese cuerpo (salvo que engorde o adelgace).
La otra fuerza es el contacto con la palangana que llamaremos normal, N. Su nombre obedece a que forma un ángulo de 90º con la superficie de la palangana. |
|
|
|
La palabra normal es sinónimo de perpendicular, recto, ortogonal (la sinonimia de las dos últimas entre sí es obvia). En este ejercicio el hecho de ser normal es suficientemente importante como para ponerle como nombre normal a la fuerza, que tiene esa dirección. En la inmensa mayoría de los ejercicios de Física, esa característica es irrelevante generalmente y ponerle ese nombre sólo alimenta la confusión de los estudiantes, pero en este caso, no.
Como ves el módulo de la normal no es constante: es mayor cuanto más abajo está rodando el cuerpo, con un máximo en la posición más baja. Incluso en algunas posiciones es mayor que el peso y en otras menor...
NC > P , NA < P
Ese es un dato interesante. Habitualmente los estudiantes creen que en el punto más bajo la fuerza que tira hacia arriba (puede también ser una cuerda, en el caso de un péndulo) es igual al peso. Y no. Es mayor porque la resultante entre ambas debe ser distinta de cero y apuntar hacia el centro de la circunferencia (en este caso hacia arriba). La Segunda Ley de la Dinámica lo predice:
ΣF = m aC
Y como en C la aceleración centrípeta es distinta de 0, la fuerza que apunta hacia el centro, N, debe ser mayor que la que apunta hacia afuera, P.
La misma línea de razonamiento nos permite conocer el módulo de la normal en otras posiciones. Pongamos por ejemplo la posición extrema de la oscilación, el punto A. El siguiente DCL describe la situación: |
|
|
 |
Tomé un eje de referencia instantáneo que tiene una dirección radial y la otra tangencial (son normales entre sí). En base a ese sistema descompongo la fuerza peso, y así quedan definidas la componente radial PR, y la componente tangencia, PT.
Como se trataba de la posición extrema, la velocidad de cuerpo debe valer cero, y por ende, la aceleración centrípeta también (acordate que aC = v²/ R) de modo que la normal es esa posición debe ser igual y contraria a la componente radial del peso: |
|
|
|
NA — PR = 0
Como ves, en este caso extremo (y sólo en él) la componente tangencial de peso es la resultante de las fuerzas.
Creo que ya estamos listos para cumplir el requerimiento del ejercicio. Acá va. |
|
|
 |
Y también podemos completar el panorama de la dinámica de este problema.
En la posición extrema, A, el cuerpo tiene velocidad cero, pero la componente libre del peso lo acelera hacia abajo. Al pasar por B, la superficie de la palangana lo desvía hacia arriba (si así no fuera, el cuerpo ya la habría perforado) lo cual implica una aceleración centrípeta... pero se sigue acelerando linealmente hacia abajo (menos que antes pero acelerando al fin) y eso hace que tenga más velocidad. |
|
|
|
Al pasar por C, la posición más baja, se extingue la aceleración tangencial. A partir de ahí reaparece, pero contraria al desplazamiento, de modo que desde ahí: comienza a frenarse.
En el punto D, podemos observar cómo continúa la fuerza frenándolo y desviándolo al mismo tiempo. Y así llega al otro extremo, E, en el que se frena completamente... pero como la resultante es tangencial a la superficie y apunta hacia abajo, el cuerpo pegará la vuelta para iniciar un nuevo recorrido. |
|
|
| |
|
|
| DISCUSION: Si realmente no hubiese rozamiento ni ninguna otra fuerza que quite energía del sistema el cuerpo se mantendría oscilando indefinidamente. Pero esas cosas no ocurren en nuestro universo, al menos en la escala de nuestras palanganas. |
|
 |
DESAFIO: ¿Cuánto valdría la resultante en C si la altura de la palangana fuese de 10 centímetros y la masa del cuerpo 1 kg? |
|
| Algunos reservados (no es que sean tímidos, callados).
Se permite su reproducción citando la fuente. Última actualización jun-08. Buenos Aires, Argentina. |
|
|
|

