NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Leyes de Newton, estática)
|
|

|
| |
 |
FIS d1.03 - Un cuerpo de masa m se encuentra en reposo,
apoyado sobre una mesa horizontal que
presenta rozamiento despreciable. Analizar, sin
hacer cuentas:
a- ¿Qué intensidad mínima tendrá la fuerza horizontal
necesaria para moverlo?
b- ¿Qué aceleración tendrá si se le aplica una
fuerza vertical, hacia arriba, de módulo igual al
de su propio peso?
c- ¿Qué aceleración tendrá si se le aplica una
fuerza horizontal, de módulo igual al de su propio
peso? |
|
OK... es muy básico, pero tal vez podamos sacarle algún provecho.
|
 |
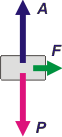
Tenemos un cuerpo apoyado sobre una mesa horizontal. No hay rozamiento entre las superficies de apoyo (rozamiento despreciable). De modo que las únicas dos fuerzas que están actuando son: su propio peso, P, que es la fuerza con que la Tierra atrae al cuerpo; y la fuerza de apoyo, A, que es la fuerza con que la mesa sostiene al cuerpo (si vos querés llamarla normal yo no me ofendo, pero tampoco te lo recomiendo) |
|
|
|
En esta situación su aceleración vale cero porque la sumatoria de fuerzas que actúan sobre el objeto también vale cero.
ΣF = m . a → A — P = 0
Ahora vamos a la primera:
a- ¿Qué intensidad mínima tendrá la fuerza horizontal
necesaria para moverlo?
No existe un valor mínimo. En teoría con una fuerza de 0,000001 N podríamos acelerar al cuerpo y moverlo. Pero claro, digo en teoría porque con una fuerza tan pequeña seguramente el rozamiento ya no sería despreciable como indica el enunciado. |
|
|
 |
Si el cuerpo tuviese una masa de 1 kg, con esa fuerza podría comunicarle una aceleración de:
a = F/m = 0,000001 m/s²
Alguien me contó una vez, que existía un mito acerca de que para mover un cuerpo era necesario aplicarle una fuerza por lo menos igual a su propio peso. Además de que eso es absolutamente falso -aún cuando entre la mesa y el cuerpo hubiese rozamiento-, nunca pude verificar que el mito existiese de verdad ¿vos creías eso? |
|
|
|
Vamos a la segunda:
b- ¿Qué aceleración tendrá si se le aplica una
fuerza vertical, hacia arriba, de módulo igual al
de su propio peso?
Tendría una aceleración nula. Seguiría quieto como antes. |
|
|
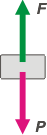 |
Tal vez protestes y digas: -Se olvidó la fuerza de apoyo que ya estaba de antes... No, no me olvidé. Ocurre que si a un cuerpo apoyado le aplicás una fuerza hacia arriba, la fuerza de apoyo disminuye a medida que la fuerza aplicada crece. Y el apoyo se hace cero cuando la fuerza aplicada hacia arriba alcanza el valor del peso.
Las fuerzas de contacto (en este caso, el apoyo) poseen una mecánica muy sutil que no viene al caso ponerme a explicar, pero que es bastante intuitiva. |
|
|
|
Vamos a la tercera y última.
c- ¿Qué aceleración tendrá si se le aplica una
fuerza horizontal, de módulo igual al de su propio
peso?
Tendría una aceleración horizontal de 10 m/s², más o menos. |
|
|
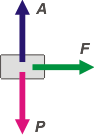 |
La explicación es muy sencilla. En la dirección x la única fuerza que actúa es la que indica el enunciado:
ΣFx = m . ax → F = m . a
Además te dicen que esa fuerza es -en intensidad- igual al peso. Entonces la ecuación de Newton queda así:
P = m . a
|
|
|
|
Pero como le ocurre a todo cuerpo en las proximidades de la Tierra, su peso es igual al producto entre su masa y la aceleración de la gravedad. Entonces:
m . g = m . a
Si cancelamos la masa, nos queda que la aceleración horizontal será igual a g, o sea, más o menos 10 m/s². |
|
|
| Ponele. |
|
 |
| |
|
| DESAFIO: Si el cuerpo pesa 10 N y se le aplica una fuerza hacia arriba de 3,54 N, ¿cuánto valdrá la fuerza de apoyo, que los normales llaman normal? |
|
| |
|
| Algunos derechos reservados.
Algunos zurdos extrovertidos. Se permite su reproducción citando la fuente. Última actualización may-13. Buenos Aires, Argentina. |
|
|
|

