NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Leyes de Newton, vínculos)
|
|

|
| |
 |
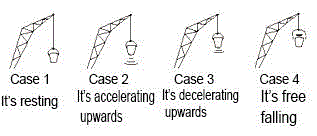
FIS d1.01- A bucket hangs from a crane's cable. Analyse the interactions that take place and draw a free body diagram for the bucket for each case. Compare the intensities between each case. If the bucket's mass was 40kg (2.2 lbs) determine the force that the cable's making, when the bucket is: |
a- Resting.
b- Going up with a velocity of 2 m/s.
c- Going up, increasing its velocity
2 m/s each second.
d- Going up, decreasing its velocity
2 m/s each second. |
 |
|
This problem's the most important one on the guide. Or it must be, because it's found countless times in different versions and situations. Look, (and if you want to, try giving each one a try and then come back) you can find it, at least, in excercises 1.4 (the next one), again in 1.13, in some additional excercises in 20, in an energy study guide. and in some others. And it's truly a really simple problem, but it caters to some basic, completely basic notions that make it difficult to keep going if you couldn't So... Pay attention.
But first I want to warn you, if you couldn't tell already, that the picture above doesn't match the items that follow. They are separate things. Once we've finished solving the problem I'll come back to the picture, ok?
In all four cases (which are very similar, dinamically speaking) there are only two forces acting. The bucket's weight, W, which is the force by which the Earth -a solid, round and wellcoming object- attracts it, as if it wanted to swallow it. And the force that the cable's doing, T, which is pulling upwards (only strings can do that: pull towards the direction they're in, they can't push or apply forces laterally). And there are no more forces! If you feel tempted to apply any other force(s)... You're screwed. I always pair this whole debate with a free body diagram.
In all cases we'll apply Newton's equation, which goes as follows: |
|
Remember that
W = m . g
so if
m = 40 kg
then
W = 400 N
|
|
|
One equation's enough because both forces are vertical. And if I take a reference frame in which the Y axis is pointing upwards, the equation's like this:
T — W = m a
In each of four cases the acceleration is different (and that'll affect the second term of the equation). Then, the only thing that can change in the first term is the force that the crane's doing, which is the cable's tension, because the bucket's weight is constant. |
|
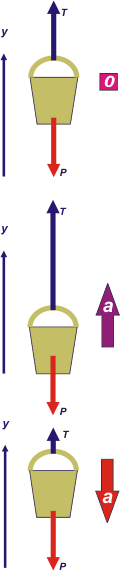 |
A and b. Both cases are identical, dinamically speaking. Acceleration is zero when the body's not moving and when it's going up or down at a constant velocity.
T — W = 0
T = W
|
|
C. Going up increasing its velocity 2 m/s each second is the same as saying it has an upwards acceleration of 2 m/s² . (In this cases, you can say, [in a very literal and argentine translation] "don't go fooling papa monkey with green bananas"... it doesn't matter, they get it.)
T — W = m a
T = m a + W
|
|
D. It's going up but slower and slower...the acceleration's going down, it'll be negative given our reference frame. (a = — 2 m/s² )
T — W = m a
T = m a + W
|
|
|
|
| DEBATE: As you can see, this is all very simple. There are only two forces present, the bigger one wins and accelerates the body towards it. That's it. It's true, I exaggerated the tension vectors' length a bit. But I did it to highlight the force that's changing in each case and its consequences. If we do it the other way round, it works just as well. In fact, in the last situation that's pictured, where it's "free falling", is not represented by any of the questions that we solved. How will it differ from the other cases? (R.: T = 0 ) |
 |
| |
| CHALLENGE: What is the cable's tension when the bucket's accelerating upwards with an acceleration equal to g? Why is it so difficult for so many people to make sense of this question? |
|
Some rights reserved. Reproduction is permitted with attribution. Translated by Melina Muleiro (my thanks to her). Last update Dec-06. Buenos Aires, Argentina.
|
|
|

