 |
NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Leyes de Newton, vínculos)
|
|

|
| |

|
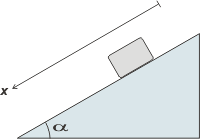
30) Un bloque de 5 kg desliza con rozamiento despreciable por un plano inclinado
recorriendo, a partir del reposo, 1 m al cabo de 2 segundos.
a) Hallar la componente del peso paralela al plano inclinado.
b) ¿Qué tiempo tardará en recorrer la misma distancia con las mismas condiciones
iniciales otro cuerpo de masa doble? |
|
|
|
El bloque puede estar subiendo o bajando... da exactamente lo mismo. Acá te lo represento bajando para que no te ocurra un cortocircuito neuronal mientras resolvemos el ejercicio. |
|
|
 |
Como siempre, tenemos que hacer un DCL, ya hí vas a ver bien a qué se refiere el enunciado cuando habla de la componente del peso paralela al plano.
A falta de uno te hice dos DCLs. El primero, como siempre es en el que consignamos la fuerzas reales que actúan sobre el cuerpo: el peso, P, y el apoyo sobre el plano, N. |
|
|
|
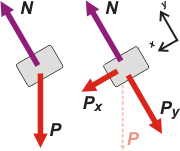 |
El segundo es el DCL útil, a los fines de aplicar la Segunda Ley, ya que al descomponer la fuerza peso en la dirección paralela y normal al plano, todas las coinciden con el SR elegido (ahí lo puse).
Px es la componente paralela al plano... y es la fuerza que acelera al cuerpo, ya que la otra componente, Py, se cancela con el apoyo del plano.
Entre P y Py, se forma, nuevamente al ángulo de inclinación del plano, α, de modo que: |
|
|
Si te cuesta entender el asunto de la descomposición de la fuerza peso, te recomiendo leer este apunte. |
Px = P sen α, Py = P cos α
Pero el problema acá es que no conocemos α, no es dato del ejercicio. En cambio nos ofrecen algunos datos cinemáticos. Vamos a aprovecharlos. Sabiendo que se trata de un MRUV, su aceleración surge de:
Δx = ½ a Δt²
De donde:
|
|
|
| a = |
|
2 Δx |
= |
2 . 1 m |
= |
0,5 m/s² |
|
|
| Δt² |
4 s² |
|
|
|
Ahora planteamos la ecuación de Newton en la dirección del movimiento:
ΣFx = m ax
Px = m ax
Px = 5 kg . 0,5 m/s²
|
|
|
|
|
|
Esto, además nos permite concluir que sobre un plano inclinado sin rozamiento, la aceleración siempre vale a = g sen α. ¿Te animás a demostrarlo?
Queda para vos el ítem b) |
|
|
| DESAFIO: ¿Qué hubiese cambiado si el cuerpo habiera estado subiendo en vez de bajando? ¿Cuánto vale el ángulo de inclinación del plano? |
|
 |
| Algunos derechos reservados (no es que sean tímidos, callados... es que si los transgredís te acuchillo).
Eso sí... se permite su reproducción citando la fuente. Última actualización jul-08. Buenos Aires, Argentina. |
|
|
|

