NO ME SALEN
PROBLEMAS RESUELTOS DE BIOFÍSICA DEL CBC
(Leyes de Newton)
|
|

|
| |

|
40- Si un avión de 2.500 kg vuela horizontalmente a velocidad constante.
|
a) ¿Cuánto vale la resultante de fuerzas sobre el avión?
b) ¿Cuál es el valor de la fuerza ascensional que el aire ejerce sobre el avión?
Este ejercicio es interesantísimo para los incrédulos. Empecemos con el DCL y presentando todas las fuerzas que actúan sobre un avión volando. |
|
|
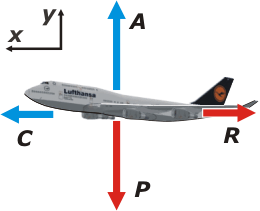 |
Por supuesto que está afectado por la atracción de la Tierra, de modo que actúa su peso, P, que en este caso vale 2.500 kgf -o mejor aún-, 25.000 N.
Pese a que la Tierra tira hacia abajo con mucha fuerza el avión no se cae porque sus alas interactúan con el aire de un modo muy especial, creando una fuerza que empuja hacia arriba y se suele llamar fuerza ascencional, o fuerza de sustentación, A. |
|
|
|
|
También actúa un rozamiento con el aire, R, que tiende a frenar al avión. Y por último una fuerza de avance que en los aviones a chorro la crean los gases que se expulsan por las turbinas, y en el caso de los de hélices el aire que las aspas empujan violentamente hacia atrás, C.
Presentadas las fuerzas, vamos a las ecuaciones de Newton. Deben ser dos, porque las fuerzas no son codireccionales. Hay que plantear una sumatoria para el eje x, y otra para el eje y. Recordá que el enunciado aclara que vuela horizontalmente a velocidad constante, de modo que las aceleraciones en ambos ejes son nulas. |
|
|
(eje x) → ΣFx = Resx = m ax → C — R = 0
(eje y) → ΣFy = Resy = m ay → A — P = 0 |
|
|
La sumatoria de las fuerzas que actúan en un eje, no es otra que la resultante en ese eje, Resx y Resy. Y la resultante total es la composición de las resultantes de cada eje. En este caso resulta obvia: |
|
|
|
|
|
| De la segunda ecuación podemos hallar el valor de la fuerza ascencional. |
|
|
|
|
|
| De las 4 fuerzas, la que implica gasto de combustibles en la fuerza de empuje, C. Para ahorrar dinero y que los pasajes sean más baratos los pilotos deben buscar lugares del cielo donde la fuerza que se opone a C, o sea R, el rozamiento con el aire, sea menor. Eso ocurre a mayores alturas (cuanto más alto nos vamos menos aires hay y por lo tanto menos rozamiento... lo que conduce a menos gasto). La pregunta inmediata es: ¿entonces por qué no vuelan donde no hay nada de aire, más hallá de la atmósfera? El problema es que los pilotos también necesitan de la presencia de aire para que haya interacción con las alas y se produzca la fuerza ascencional, A. Es lo que en física o en ingeniería se conoce como una situación de compromiso. Se resuelve de manera práctica observando a qué altura hay menor consumo, mayor velocidad y suficiente sustentación. El resultado es que, para viones comerciales, esa altura ronda los 10.000 metros sobre la superficie terrestre. No es capricho. |
|
|
|
|
|
| PARA APRENDER MÁS. Tenés una explicación alternatica acá. |
|
 |
| Algunos derechos reservados (no es que sean tímidos, callados... es que si los transgredís te acuchillo).
Eso sí... se permite su reproducción citando la fuente. Última actualización mar-20. Buenos Aires, Argentina. |
|
|
|

