NO ME SALEN
THEORETICAL NOTES AND EXERCISES OF PHYSICS AND BIOPHYSICS
Dynamics

NEWTON'S LAW

The Newton's law, attributed to Isaac Newton (1643-1727), have, actually, too many authors. But it was Newton who exploited them and use them together, making the Mechanic Theory (known now a days as the Clasic Mechanic) which enjoys perfect health and we still use with success.

As well as its proven utility, and eficacy it constitutes an example archetypal of theory, highlighted by its intrinsic beauty, because with few algebraic premises, we get to an explanation really precise about the universe.

Their are four laws altogether. Their are also called principles because you can't prove them based on old laws or more basic ones, but the universe carry out in perfect order, even when we really don't know why. I am going to present the first three here, and the fourth, universal gravitation, on another note.

First law of motion, or Law of Inertia, or Galileo's Principle

You already figured out who finded them out before Newton. There are dozens of alternative versions. Here is mine.

If over a body no force is applied, or a lot of forces are applyed but the compensate each other, then the body will remain still or in uniform linear motion . And viceversa.

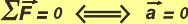Below there is a super important gossip about this Principle.

Second law of Motion, or Mass Law, or Newton's principle

It's called Mass Law, because the mass itself, that property of the matter which nobody knows what is really is (below there is a gossip about mass), has an important role.

The sum of all the forces applied on a body is equal to the product of the body's mass times its acceleration.

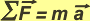The Second Law is a vectorial equation: the sum of all the forces that a body receives is equal the product of its mass times its accelaration, and the direction and sense of its accelaration (the mass is a scalar). Nevertheless, in many texts (including this) this expression might be used but without using vectorial notation, like this: ΣF = m a. It is forgivable, can't bring us too much consequences.

What is unforgivable is that in plenty of text the Law is presented like this:

F = m a (bad, horrible, immoral, criminal, hateful!!!)

That expression is valid in only one case, when there is only one force acting on a body. It cannot be presented as a Law (eternal, and universally valid). Besides, it confuses ourselves negatively: it makes us believe that is a force's property (like if each force had its own acceleration), when we are dealing with a property of the bodies. The law is applied to every body, not to every force.

In that case, represent it like this: R = m a, clarifying that R is the (resultante) and it can't be another thing that the summatory of all the forces acting on a body. R = ΣF.

Third Law of Motion, or Action-reaction Law.

If a body applies a force on another, this one applies the same force but on the first one and with the same modulus, direction and opposite sense than the first one did on the second.

Considering the three principles, this one details best the natures of the forces. Actually, we should be talking about interaccions. Between two bodies, they always: attract, or repel, or push, or touch, or crash themselves, or whatever... but always between two bodies. So, two forces appear (el par de fuerzas de interaccion), one in each body that is interacting.

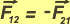It seems that the universe is a pandemonium of revenges, in which the Tailon Law rules.

Important gossips:

• From the first point of view, it seems that the first principle is a particular case of the second. Indeed, basing ourselves by the second law, ΣF = 0, what has to be 0 is accelaration, since the mass cannot be zero... Nevertheless, the first principle is the one that guarantees the existences of the other two, and demands the reference system to be carryed out correctly. It may happen that the selection of the reference system takes us to an universe in which the Newton's Law can't be applied. Those systems, are called Non Inertial Systems. Leave it there, they aren't neccesary now.

• Both mass and force are magnitudes really difficult to understand. Defining only one of these is enough, because the other one will come out using the Second Law. Poor Newton died sad knowing that there was a flaw in his theory: the absence of definition of this two important magnitudes. 200 years had to pass until physicist Ernst Mach (1838-1916) could reach a definition about mass that could convince the cientific community. Nevertheless, Newton arranged prefectly an idea about the concept of mass: a scalar -a number- that indicates the amount of matter a body is made of.

• One of the inferences about the Action-reaction Principle, is that the (pares de interaccion) are never applied on the same body. Their are always applied on different bodies (the ones interacting).

• If every time that a force appears, another one appears with the same modulus but opposite... How is it possible for things to move?  
  

• If a butterfly crushes into the windshield, the force that other make to each other has the same intensity... Then why the butterfly smashes into the windshield and the windshield y safe and sound?
  

• Which aspect of Ernst's definition of mass inspired Einstein's General Theory of Relativity.