NO ME SALEN
EJERCICIOS RESUELTOS DE FÍSICA DEL CBC
(movimiento relativo)
|
|

|
NMS c7.22* - Un avión debe volar desde una localidad A hacia otra B ubicada 2250 km en dirección N 37° E, en un día en que sopla un viento muy fuerte de Este a Oeste. Para lograrlo el piloto orienta el avión en dirección N 53° E, desarrollando una velocidad constante respecto del viento de módulo igual a 600 km/h.
a) ¿Cuánto tiempo demora el avión en realizar el viaje?
b) Determine el módulo de la velocidad del viento respecto a la Tierra. |
*El presente ejercicio formó parte del examen parcial de Física (03) del CBC, UBA, tomado el 27-09-19. |
|
|
|
Cuando corregí este ejercicio encontré que ningún estudiante (alrededor de 40) había podido realizar el gráfico de suma de velocidades. ¡Y es lo fundamental! |
|
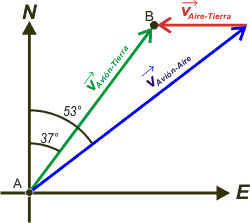
Si leés detenidamente el enunciado verás que los tres vectores de velocidad implicados en este ejercicio (como en cualquier otro de movimiento relativo) responden exactamente a lo que está escrito.
Además, se ve muy claramente el orden de la suma de velocidades de Galileo:
VAvión-Tierra = VAvión-Aire + VAire-Tierra
(suma vectorial)
De las tres velocidades la única que se conoce es la del avión en el aire, que vale 600 km/h. |
|
|
|
Hay varias maneras de resolver este ejercicio, pero si se hace correctamente el esquema de la suma vectorial se torna enormemente sencillo resolviéndolo a partir de relaciones geométricas.
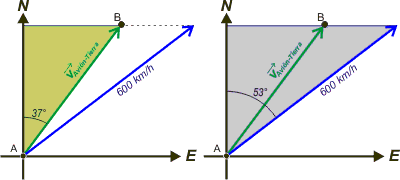
Las componentes N-S de las velocidades del avión, tanto respecto a Tierra como respecto al aire son idénticas, y fáciles de calcular. Mirá estos dos triangulitos que sombreé separadamente: |
|
Ambos triángulos son rectángulos. Y en ambos la hipotenusa es una de las velocidades, y en cada uno, el cateto N-S es el adyacente al ángulo indicado por el enunciado. |
|
|
|
Por lo tanto:
VAvión-Tierra . cos 37˚ = 600 km/h . cos 53˚
VAvión-Tierra = 600 km/h . 0,6 / 0,8
VAvión-Tierra = 450 km/h
Sabiendo con qué velocidad se mueve el avión sobre la Tierra es fácil calcular cuánto tardará en recorrer los 2.250 km que separan las localidades A y B.
ΔtAB = ΔrAB / VAvión-Tierra
ΔtAB = 2.250 km / 450 km/h
|
|
|
|
De la misma manera, si ahora observás los catetos O-E de los triángulos sombreados, o sea, los catetos opuestos a los ángulos indicados por el enunciado, se ve claramente que:
VAvión-Tierra . sen 37˚ = VAvión-Aire . sen 53˚ + VAire-Tierra
De donde:
VAire-Tierra = 450 km/h . 0,6 — 600 km/h . 0,8
|
|
| |
VAire-Tierra = 210 km/h |
en módulo |
|
|
|
|
| Desafío: ¿Con qué ángulo (respecto a la dirección N-S) debería viajar el piloto si el viento soplase en el sentido opuesto? |
 |
| |
| |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización oct-19. Buenos Aires, Argentina. |
|
|
|

