 |
NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA
(Movimiento relativo)
|
|

|
| NMS c7.15* – Durante una tormenta las gotas de lluvia observadas desde la ventana de un tren cuya velocidad es de 15 km/h forman un angulo de 30º con la vertical. Cuando la velocidad del tren aumenta en 30 km/h el angulo de las gotas con la vertical es de 45º. Si el tren estáse quieto, ¿cuál seria el angulo de las gotas de lluvia con la vertical ? Determina también la velocidad de las mismas con respecto al suelo. |
|
En este, como en todos los problemas de movimiento relativo, tenemos que encontrar tres personajes, ¿los tenés presentes? Queda claro que para un observador que está afuera del tren las gotas caen con cierta inclinación, que deberemos encontrar, pero que no caen verticalmente. Ese es nuestro observador fijo (que observa la velocidad de las gotas desde la Tierra, VG, y también la velocidad del tren desde la vereda, VT). El móvil son las gotas, y el observador móvil es el pasajero del tren (el que observa las gotas desde la ventanilla, VGT).
NOTA: las gotas de lluvia viajan a velocidad constante, al menos cuando están a nuestra vista llegando al piso. Eso se debe al rozamiento con el aire. No se trata de caídas libres ni movimientos variados.
Además tenemos dos momentos que son cuando el tren viaja a 15 km/h -que llamaremos 1- y cuando el tren viaja a 30 km/h -que llamaremos 2-. Acá viene lo principal del ejercicio... cuando podés traducir el enunciado a un esquema de suma de vectores (en este caso a dos). |
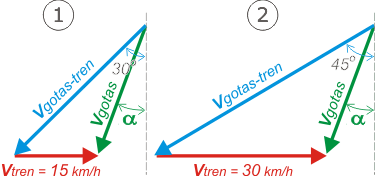 |
|
Los esquemas no están hechos a escala. |
La velocidad de las gotas respecto de la Tierra, VG, y el ángulo que forman con la vertical, α, son los mismos en ambos casos. Son los valores que tenemos que averiguar. En ambos se dará que:
VG = VGT1 + VT1 vectores
VG = VGT2 + VT2 vectores
Escribamos las mismas ecuaciones pero para sus componentes horizontal y vertical (usaré sentido positivo hacia la izquierda y hacia abajo):
1 vertical VG cos α = VGT1 cos 30°
1 horizontal VG sen α = VGT1 sen 30° — VT1
2 vertical VG cos α = VGT2 cos 45°
2 horizontal VG sen α = VGT2 sen 45° — VT2
Si lo mirás con cariño tenés ahí 4 ecuaciones con 4 incógnitas. Yo te lo resuelvo (hay 28.319 caminos diferentes, y no tengo idea si el que voy a recorrer yo es el más elegante). Lo importante es que entiendas que acá se acabó la física y tenés que arremangarte con el álgebra.
Como las velocidades de la gota respecto al tren no nos interesan las despejamos de la primera y la tercera ecuación:
VGT1 = 1,155 VG cos α
VGT2 = 1,414 VG cos α
Lo que nos dio lo metemos en la segunda y en la cuarta respectivamente.
VG sen α = 0,577 VG cos α — 15 km/h
VG sen α = VG cos α — 30 km/h [1] (esta la volveré a usar)
Igualemos los segundos miembros:
0,577 VG cos α — 15 km/h = VG cos α — 30 km/h
Simplifiquemos un cacho:
VG cos α = 35,5 km/h [2]
Si metemos eso en la ecuación [1]
VG sen α = 5,5 km/h [3]
Ahora divido miembro a miembro la [3] con la [2]:
tg α = 0,154
|
|
cos 30°=0,866
sen 30°=0,5
cos 45°=0,707
cos 45°=0,707 |
| |
α = 8,75° |
inclinación de la lluvia |
|
|
|
Vuelvo a la [2] o a la [3] (o mejor a ambas)...
|
|
|
| |
VG = 35,9 km/h |
velocidad de la lluvia |
|
|
|
Aunque no nos lo piden, podemos averiguar la velocidad de las gotas vistas desde el tren cuando se mueve a distintas velocidades:
VGT1 = 40,1 km/h cuando viaja a 15 km/h
VGT2 = 50,2 km/h cuando viaja a 30 km/h
|
|
|
| NOTA: este ejercicio admite dos soluciones, ya que podría ocurrir que el viento vaya en sentido contrario al movimiento del tren (como lo desarrollé acá) o en el mismo sentido, caso en que cambian ambos resultados. |
|
|
| *Este interesante problema me lo envió Rodrigo Benítez, hincha de San Lorenzo, pero no sé de dónde lo sacó. |
|
|
|
DESAFIO: Si hiciste el desarrollo algebraico conmigo te eximo del desafío. Si no... tu desafío es hacer uno alternativo y mandármelo si te parece que el tuyo es más económico y elegante. |
|
 |
| Algunos derechos reservados.
O sea: propiedad intelectual, propiedad vertical y propiedad horizontal. Se permite su reproducción citando la fuente. Última actualización jun-14. Buenos Aires, Argentina. |
|
|
| |
|

