 |
NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA
(Movimiento relativo)
|
|

|
| NMS c7.11- Un piloto de un avión desea volar a una ciudad 400 km al NO de su origen. Si sopla un viento de 50 km/h en dirección SSO y el avión tarda 1 hora y 47 minutos en llegar a destino, ¿Con qué velocidad se desplaza el avión por el aire? |
 |
|
Este ejercicio de movimiento relativo incluye la dificultad de que los vectores velocidad no son unidireccionales ni forman 90 grados dos de ellos cualquiera. De modo que el triángulo que se forma con su suma (o su resta) no es rectángulo y no podés valerte del teorema de pitágoras. Se nos veda la resolución geométrica. En horabuena.
Por supuesto, aunque no se trate de un tópico de la Física, no se puede interpretar el enunciado si no se conoce la roseta de los vientos. Por si las moscas, te coloqué una al lado del enunciado. |
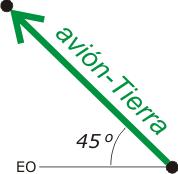 |
Mirá estos esquemitas que nos muestran el vuelo del avión en la dirección NO (noroeste).
Asumamos que el piloto es experto (todos lo son) entonces colocará la nariz del avión en una dirección diferente (volará hacia otro lado) de forma tal que la acción del viento lo lleve directamente y en línea recta hacia su destino que se halla exactamente al NE de su partida.
Por lo tanto la velocidad del avión, valga lo que valga tendrá la misma dirección que su desplazamiento y llegará felizmente a destino. |
|
|
|
Según el código de colores que vengo utilizando en estos ejercicios a la velocidad del móvil respecto del sistema fijo le toca el verde, y la llamaré VAT. Y queda claro que forma un ángulo de 45 grados con el eje E-O. El módulo de la velocidad es fácil de obtener, ya que se desplaza a velocidad constante y recorre 400 km en 1,78 h, de modo que:
|
|
|
| VAT = |
|
Δr |
= |
400 km |
|
|
|
| Δt |
1,78 h |
|
|
|
VAT = 224 km/h
Veamos qué pasa con el viento. |
|
|
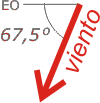 |
El viento apunta hacia el SSO (sur-suroeste), o sea, su dirección forma un ángulo de 67,5 grados con la dirección O-E (justo en la bisectriz entre S y SO, o sea: 45 más la mitad de 45).
Sabemos que el módulo de esa velocidad es de 50 km/h. La voy a llamar VVT (por: velocidad del viento medido desde la Tierra) |
|
|
|
Con esos dos vectores, ya podemos imaginar hacia dónde debe apuntar la nave el piloto. O sea, ya podemos imaginar el vector velocidad del avión en el aire, VAA, y podemos formar (a ojo y sólo a para aportar claridad, no para hacer cálculos) el triángulo suma vectorial. Nos queda una cosa parecida a ésta. Fijate si estás de acuerdo. |
|
|
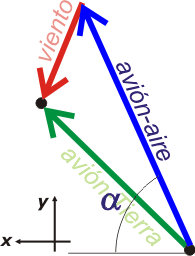 |
Según la ley de adición de velocidades de Galileo, podemos asegurar que:
VAA + VVT = VAT
Disculpá que no tengo flechitas para destacar el carácter vectorial de esa suma. Para resolverla tendremos que descomponer esas velocidades en sus direcciones E-O (x) y N-S (y).
De modo que tendremos dos sumas en lugar de una:
VAAx + VVTx = VATx
VAAy + VVTy = VATy
Si llamamos α al ángulo que la velocidad del avión respecto del aire forma con el eje x, las dos sumas quedan así: |
|
|
|
VAA cos α + VVT cos 67,5° = VAT cos 45°
VAA sen α — VVT sen 67,5° = VAT sen 45°
Reemplacemos el resto de los datos a ver qué queda (te lo hice en dos pasos para que no te pierdas):
VAA cos α + 50 km/h 0,383 = 224 km/h 0,707
VAA sen α — 50 km/h 0,924 = 224 km/h 0,707
Como ves, en definitiva tenemos dos ecuaciones con dos incógnitas, y esto tiene solución. Yo te lo hago. primero un poco de limpieza:
VAA cos α + 19,13 km/h = 158,37 km/h
VAA sen α — 46,19 km/h = 158,37 km/h
Sigo limpiando:
VAA cos α = 139,24 km/h
VAA sen α = 204,56 km/h
Ahora divido miembro a miembro la ecuación de abajo por la de arriba:
tg α = 1,469
de donde, redondeando:
α = 55,75°
Reemplazamos esto en ambas ecuaciones (para corroborar que llegamos al mismo resultado). Y obtenemos la respuesta. |
|
|
|
|
|
| En el ejercicio siguiente (en esta guía) repito el que acabamos de resolver pero ofreciendo como dato la velocidad del avión en el aire, y preguntando con qué velocidad se desplaza visto desde Tierra. Vas a ver qué diferentes que resultan las dificultades algebraicas entre una resolución y la otra y cuán idénticos son en su aspecto físico. |
|
|
DESAFIO: Hacé un esquema de los movimientos con las velocidades y sus proyecciones. |
|
 |
| Algunos derechos reservados. Algunos izquierdos también. O sea: propiedad intelectual, propiedad vertical, propiedad horizontal y la propiedad del prójimo. Se permite su reproducción citando la fuente, o sea a mí. Última actualización abr-11. Buenos Aires, Argentina. |
|
|
| |
|

