 |
NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA
(Movimiento relativo)
|
|

|
 |
NMS c7.08- La escalera mecánica instalada en un «shopping» traslada a los visitantes desde planta
baja hasta el piso superior, 3,6 m más arriba.
La cadena de escalones se mueve ascendiendo
en una dirección que forma 37° con la horizontal,
a 30 cm/s. Cada escalón tiene 30 cm de altura.
Determinar, para cada uno de los personajes
siguientes, cuánto tiempo tardarán en trasladarse
desde un piso hasta el otro, y cuántos escalones
pasarán bajo sus pies. |
|
a - Susana se para en un escalón, y se deja llevar
por la escalera hasta arriba.
b - Carlos trepa por la escalera, a razón de un
escalón por segundo.
c - Jaimito baja la escalera, a razón de un escalón
por segundo.
d - El mecánico de mantenimiento detiene la
escalera, y sube por ella a razón de dos escalones
por segundo.
Este ejercicio es paradójico. Es tan sencillo que lo podría resolver cualquier transeúnte del shopping, con la condición de que se lo preguntemos haciéndole creer que es por el concurso para un viaje al Caribe con su estrella favorita. En cambio, si llega a sospechar que se trata de física, cinemática o movimiento relativo... olvídalo.
En clase me resisto a explicarlo... y le digo a mis estudiantes: pensalo, y si no lo sacás te reviento a golpes. Pero parece que esa insinuación los hunde todavía más en la mística académico-científica, y ahí sucumben. En el shopping lo resolverían sin siquiera darse cuenta, ni festejar. Voy a resolverlo de dos maneras diferentes y trataré de mostrarte todos los caminos mentales que podrías tomar.
La primera forma de resolver este problema es la que intentaría un estudiante desesperado por aprobar la materia, temeroso, pero valiente: vamos a exprimir los datos del problema a ver qué otras informaciones esconden y les podemos sacar.
|
|
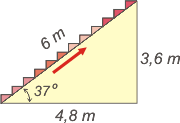
Ahí tenés la escalera mecánica, entre los dos pisos del shopping. Con la diferencia entre pisos, Δy = 3,6 m, y el ángulo de inclinación de la escalera, suponemos que cualquier estudiante universitario (no un transeúnte) puede calcular las dimensiones que faltan.
Usando la tangente de 37° sale el desplazamiento lateral, Δx = 4,8 m. Y con la función seno, el largo de la escalera o desplazamiento sobre la diagonal, que realiza cada escalón, que vale Δl = 6 m. |
|
|
|
|
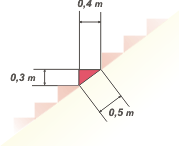
Si pudiste con eso, también podrás con las medidas de un escalón cualquiera (son todos iguales). El dato es los 0,3 m de altura. Operando de la misma manera que antes, obtenemos las dimensiones faltantes que son: 0,4 m de ancho (suficiente para un pie de Carlos) y 0,5 m de diagonal, por la que asciende suavemente hacia los locales de arriba donde se vende en cómodas cuotas con VISA o American Express. |
|
|
|
Resulta fácil darse cuenta de que a lo largo de la escalera hay 12 escalones siempre al descubierto. Elijas la dimensión que elijas para efectuar el cálculo, el cociente vale 12. ¿Hacés la prueba? 3,6 m de altura total dividido 0,3 m de altura de cada escalón da 12. Con las otras dimensiones lo mismo. Hacelo, así vas calentando las neuronas.
Pasemos a la cuestión de las velocidades. La frase "La cadena de escalones se mueve ascendiendo
en una dirección que forma 37° con la horizontal,
a 30 cm/s" (tenés derecho a leerla 59 veces) quiere decir que la velocidad de avance sobre la diagonal (esa que yo te pinté en rojo en el primer esquema de ahí arriba) vale 30 cm/s. Podríamos llamarla velocidad de la escalera, ¿dale? Y como es mi costumbre la voy a representar en rojo, ya que se trata del medio móvil.
VE = 30 cm/s = 0,3 m/s
Para atravesar toda la cinta de deslizamiento, un escalón tardará:
Δt = Δl / VE = 6 m / 0,3 m/s = 20 s
Nada mal para ir preparando la billetera. Pero volviendo a la cinemática, razono que si 12 escalones desaparecen en 20 segundos en el piso de arriba (o aparecen en el de abajo), eso quiere decir que aparecen a razón de 0,6 escalones por segundo. Todo esto no te lo digo para confundirte. Es sólo un razonamiento más que se te podría ocurrir, y si no le ves utilidad dejalo ahí anotado en el margen... papel es lo que sobra. |
|
|
|
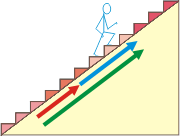
Acá tenés la situación relativa. La escalera mecánica es un espacio móvil, que permite movimientos adentro suyo. La persona camina sobre la escalera con una velocidad típica de su temperamento y su musculatura. Su velocidad la llamaré VP (velocidad de la persona); y desde los locales de arriba se estarán relamiendo porque ven que la persona llega más rápido a comprar... a esa velocidad resultante la llamaré VS (velocidad vista desde el shopping). |
|
|
|
Como enseñó Galileo, se cumple que:
VS = VP + VE
Ahora basta con reemplazar la velocidad de la persona por cada una de las personas que aparecen en el enunciado. Se agrega la pequeña dificultad de encontrar el valor de esas velocidades porque no vienen expresadas en metros ni centímetros sobre segundo sino en "escalones por segundo". Pero si miramos una vez más el esquemita del escalón, resulta obvio que subir un escalón por segundo es lo mismo que ascender 0,3 m por segundo... o desplazarse lateralmente 0,4 m por segundo... o -lo que a nosotros nos interesa- desplazarse en diagonal, sobre la escalera, a razón de 0,5 m por segundo.
Según mis cálculos, las velocidades de las personas son:
velocidad de Susana, VPS = 0 e/s = 0 m/s
velocidad de Carlos, VPC = 1 e/s = 0,5m/s
velocidad de Jaimito, VPJ = –1 e/s = – 0,5m/s
velocidad del mecánico, VPM = 2 e/s = 1 m/s
Ahora, a cada uno por separado le sumo la velocidad de la escalera, y así obtengo la velocidad con que los ven subir en el shopping.
VSS = VPS + VE = 0 m/s + 0,3 m/s = 0,3 m/s
VSC = VPC + VE = 0,5m/s + 0,3 m/s = 0,8 m/s
VSJ = VPJ + VE = – 0,5m/s + 0,3 m/s = – 0,2 m/s
VSM = VPM + 0 = 1 m/s
Para saber lo que tarda cada uno, volvemos a la definición de velocidad (constante):
|
|
|
ΔtS = Δl / VSS = 6 m / 0,3 m/s = 20 s
ΔtC = Δl / VSC = 6 m / 0,8 m/s = 7,5 s
ΔtJ = Δl / VSJ = – 6 m / – 0,2 m/s = 30 s
ΔtM = Δl / VSM = 6 m / 1 m/s = 6 s |
|
|
|
Ese es el tiempo que cada uno permanece arriba de la escalera. Una forma de averiguar cuántos escalones pasaron bajo sus pies es multiplicar ese tiempo por la velocidad de cada uno (medida en escalones por segundo). El caso de Jaimito no es para preocuparse. Sólo se divierte (si vos no lo hiciste nunca es porque no tuviste infancia). |
|
|
#eS = 20 s . 0 e/s = 0 e
#eC = 7,5 s . 1 e/s = 7,5 e
#eJ = 30 s . 1 e/s = 30 e
#eM = 6 s . 2 e/s = 12 e |
|
|
|
Bueno, hasta aquí el problema, más o menos como lo haría yo en un curso de Física en el que intento enseñar cinemática, y movimiento relativo. |
|
|
|
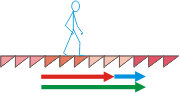
Inclusive te puedo explotar un poco más las ideas que expuse hasta aquí, y resolver exclusivamente usando la velocidad de traslación horizontal de la escalera, la horizontal de avance de las personas. Si hago eso, el cambio de piso (de planta baja a primero) se logra cuando la persona avanza 4,8 m. |
|
|
 |
Y por qué no... podemos plantear íntegramente el problema resolviéndolo con velocidades verticales. En ese caso, el cambio de piso se logra cuando las personas ascienden Δy = 3,6 m.
En cualquier caso, lo que tenés que tener claro es que no podés mezclar velocidades reales con sus componentes, ya sea la horizontal como la vertical. Si tenés dudas sobre a qué me estoy refiriendo te voy a dar los valores de las componentes de la velocidad de la escalera:
VEx = 24 cm/s; VEy = 18 cm/s. ¿Cazaste? |
|
|
|
De lo que no cabe duda es de que nuestro transeúnte no lo resolvería de ninguno de los modos anteriores. El lo haría aplicando simples reglas de tres y contando escalones.
Por ejemplo, para Carlos podría plantearse algo como: la escalera avanza a razón de 12 escalones cada 20 segundos y Carlos sube 1 escalón por segundo, o 20 escalones en 20 segundos. De modo que en 20 segundos estaría 32 escalones más arriba (los 20 que sube él más los doce que sube la escalera sola). Pero él no necesita ir tan alto, ni subir durante tanto tiempo. Para cambiar de piso le alcanza con 12 escalones, de modo que
32 escalones _________________ 20 segundos
12 escalones _________________ x
x = 12 escalones . 20 segundos / 32 escalones
x = 7,5 segundos
Hay decenas de planteos posibles para cada móvil; la regla del almacenero es infalible. |
|
DESAFIO: Volvé a resolver el ejercicio de las dos formas que mencioné antes: todos movimientos horizontales, y todos movimientos verticales. Después vení a buscar tu pasaje al Caribe, 7 días y estadía pagos. |
|
| Algunos derechos reservados.
O sea: la propiedad intelectual, la propiedad vertical y la propiedad horizontal. Se permite su reproducción citando la fuente. Última actualización may-07. Buenos Aires, Argentina. |
|
|
| |
|

