 |
NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA
(Movimiento relativo)
|
|

|
 |
NMS c7.03- Un bote cruza un río de 60 m de ancho con
una velocidad de 4 m/s respecto del agua, orientada
de tal forma que, si las aguas estuvieran
quietas, cruzaría perpendicularmente a las orillas.
El bote parte de un punto A ubicado sobre
una de las márgenes y llega a otro punto B en la
margen opuesta, distante 100 m de A. ¿Cuál es el
módulo de la velocidad del bote respecto de tierra
y cuánto tarda en cruzar el río? |
a) 5,33 m/s y 25 s b) 5,33 m/s y 15 s c) 5,33 m/s y 10 s
d) 6,66 m/s y 25 s e) 6,66 m/s y 15 s f) 6,66 m/s y 10 s
|
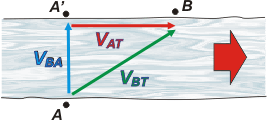 |
Vamos a repasar un poquito así te familiarizás con la nomenclatura y los subíndices. A la velocidad del río, que representé en rojo, la llamé VAT (velocidad del agua vista desde la Tierra). A la velocidad del bote en el agua, VBA (velocidad del bote vista desde el agua). Y a la velocidad del bote vista desde la orilla, VBT (velocidad del bote vista desde tierra firme). |
|
| |
Galileo Galilei advirtió por primera vez que se cumple esta ley vectorial entre las velocidades. Si sos cuidadoso en el uso de los subíndices, verás que se forma un sanguchito donde el medio móvil (en nuestro caso el agua) es el jamón (BT y BAAT).
VBT = VBA + VAT
|
|
|
Por un lado tenemos que
VBT = AB / Δt
VBA = AA' / Δt
VAT = A'B / Δt
|
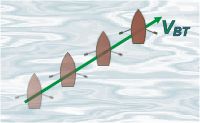 |
Así se ve al bote avanzar si estás afirmado a la Tierra (desde arriba de un puente, por ejemplo). |
|
|
|
y es dato del problema que VBA = 4 m/s entonces
AA' / Δt = 4 m/s ⇒ Δt = AA' / 4 m/s
Δt = 60 m / 4 m/s
Δt = 15 s
Ahora que sabemos cuánto tarda en cruzar el río, también podemos saber con qué velocidad lo ven cruzar desde la orilla.
VBT = AB / Δt = 100 m / 15s
VBT = 6,66 m/s
|
|
|
|
|
|
Ya que estamos... Si reemplazamos en la ecuación de Galileo las tres definiciones de velocidad (recordá que son constantes) y cancelamos Δt (operación absolutamente lícita ya que Δt es sólo un número, una magnitud escalar) lo que nos queda es una relación entre tres segmentos, AB, AA' y A'B, que forman un triángulo rectángulo y que por lo tanto entre ellos se verifica el Teorema de Pitágoras. No tenés que hacer pucheros... los triángulos amorosos son mucho más difíciles de resolver que los triángulos rectángulos.
AB es la hipotenusa y vale 100 metros. AA' es el cateto menor y vale 60 metros. A'B es el cateto mayor y no sabemos cuánto vale, pero la calculadora seguro que sí.
A'B² = AB² – AA'²
A'B² = 80 m
Si hacemos lo mismo con las velocidades, verificamos que |
|
|
| VAT = |
|
A'B |
= |
80 m |
= 5,33 m/s |
|
|
| Δt |
15 s |
|
|
|
y también
VBT² = VBA² + VAT ²
Todo cierra. Ojo, esto vale sólo para este problema y para aquellos otros en los que el docente sea tan gentil de poner dos velocidades normales entre sí. Nada lo obliga. |
|
|
| |
|
 |
| Algunos derechos reservados, otros extrovertidos.
Se permite su reproducción citando la fuente, o sea... el de la foto. Última actualización set-06. Buenos Aires, Argentina. |
|
| |
| |
|

