 |
NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA
(Coordenadas intrínsecas, radio de curvatura)
|
|

|
 |
Nc6.20 - La órbita de un planeta alrededor del Sol
es una elipse, en la cual el Sol ocupa uno de los
focos.
Sabiendo que la aceleración del movimiento
del planeta está dirigida en todo instante hacia el
Sol, determinar si su velocidad puede ser constante,
y hallar en qué posiciones adquiere su módulo
máximo y mínimo, respectivamente. |
|
 |
|
|
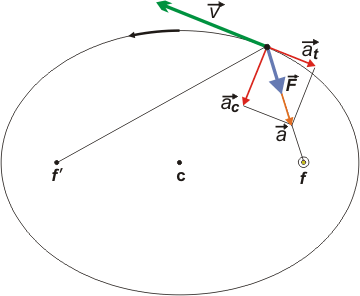
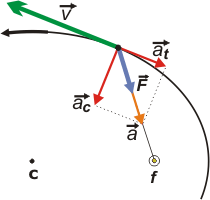
Cómo hacemos para entender este gráfico; tomalo con calma. La elipse tiene dos focos y en uno de los focos (f) está el Sol. En el otro foco no hay nada (pero podríamos inventar que hay un anti-Sol, ¿dale?). Bueno, ejemm... En azul te dibujé la fuerza con la que el Sol tiene atrapados a los planetas. Esa fuerza se estudia con cierto detalle en el capítulo fuerzas gravitatorias. En la misma dirección y con el mismo sentido (obedeciendo la segunda Ley de Newton, ΣF = m a) dibujé la aceleración, a, del planeta, en naranja.
La aceleración se puede descomponer en dos direcciones: una dirección paralela a la velocidad, v, del planeta en ese instante y otra dirección perpendicular a la anterior hacia el lado interno de la curva. Se llaman aceleración tangencial (at) y aceleración centrípeta (ac), respectivamente. A esas dos componentes las dibujé en rojo.
La velocidad de cualquier móvil, SIEMPRE, es tangente a la trayectoria, y la aceleración centrípeta SIEMPRE es perpendicular a la trayectoria. Pero fijate vos... la aceleración centrípeta NO NECESARIAMENTE APUNTA AL CENTRO DE LA ELIPSE, (C). Eso tiene consecuencias muy interesantes. Después retomo sobre este asunto.
|
|
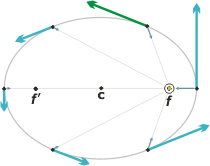
Bien, como se ve en el gráfico, la aceleración tangencial nos está diciendo, o describiendo, que la velocidad está cambiando de módulo; en particular: está disminuyendo. Esto contesta parte de la pregunta del enunciado. Depende de vos, de las construcciones geométricas que hagas, o de tu imaginación, que te des cuenta en qué posiciones -durante su recorrido a lo largo de la elipse- el planeta posee una aceleración tangencial contraria al sentido de giro (como en el caso representado arriba), o a favor del sentido de giro... o incluso cuándo su aceleración tangencial vale cero. En un caso irá cada vez más lento y, en el otro, cada vez más rápido. |
|
|
|
|
Las elipses son figuras de gran elegancia matemática. Cuando Kepler descubrió que las órbitas planetarias eran elipses, todo el mundo quedó con la boca en forma de elipse.
Además de tener dos focos, toda elipse tiene un centro, que se halla en el punto medio entre los focos. Cuanto más separados estén los focos más "aplastada" es la elipse, más excéntrica, decimos nosotros. Cuanto menos excéntrica es una elipse más se parece a una circunferencia. |
|
 |
La aceleración centrípeta del planeta no apunta al centro, justamente porque la elipse es excéntrica. Eso hace justamente que no "doble" siempre igual: a veces va más derecho y, a veces, hace la curva más pronunciada.
Pero volvamos a la velocidad. Como ya vimos, su módulo no es constante; y si razonaste correctamente, encontraste que va más rápido en las cercanías del Sol y más lento cuanto más lejos de éste se halle. De hecho el máximo lo
obtiene en la posición más cercana al Sol que se llama perihelio, y el mínimo en la más lejana, afelio. |
 |
| |
 |
Las órbitas de los planetas del Sistema Solar son tan poco excéntricas que a simple vista parecen circunferencias. Por lo tanto la diferencia de velocidad entre el perihelio y el afelio es muy pero muy pequeña. Los cometas, en cambio, tienen órbitas muy excéntricas y el foco vacío les queda muy pero muy lejos, así que cuando llegan al barrio de los planetas pasan zumbando, y cuando se van a los suburbios se mueven tan despacio que tardan muchísimo en regresar (por suerte). |
|
|
DESAFIO: Buscar en la web "kepler segunda ley", leer un cacho, y tratar de relacionarlo con esto. |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización dic-06. Buenos Aires, Argentina. |
|
|
|

