 |
NO ME SALEN
EJERCICIOS RESUELTOS DE FÍSICA
(Movimiento circular)
|
|

|
| |
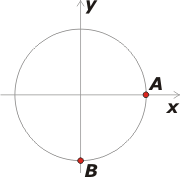
FIS cN6.19* - Una motocicleta que parte del reposo desde el punto A realiza un movimiento circular uniformemente variado en sentido antihorario. Tarda 2 segundos en pasar por primera vez por el punto B. En ese instante el ángulo que forman los vectores aceleración y velocidad es, aproximadamente, de:
a) 90˚ b) 84˚ c) 53˚
d) 37˚ e) 9˚ f) 0˚
|
 |
|
| *Este ejercicio formó parte del final de Física tomado el 29 de noviembre de 2019. |
|
|
|
Ejercicio para expertos... pero es fácil, no te asustes. Lo importante es tener claro qué es lo que te preguntan y cómo harías para resolverlo. Si lográs eso yo me doy por satisfecho, con eso me conformo... de última te copiás del compañero de al lado.
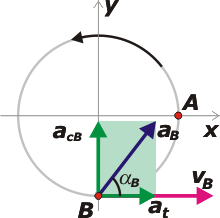
La aceleración en B es la resultande de sus componentes centrípeta y tangencial. Tenés que hallarlas por separado y recordar el carácter vectorial de esas aceleraciones para encontrar el ángulo que te solicitan. Mirá el esquema: |
|
|
Ahí tenés los vectores de aceleración tangencial, at, que es constante porque el movimiento es uniformemente variado, y que -su nombre lo indica- es paralelo a la velocidad (en rosa); El vector aceleración centrípeta, acB, que va variando a medida que la motocicleta va aumentando su velocidad (por eso lleva el subíndice B); y la composición de ambas, la aceleración en B, aB, cuyo ángulo con la velocidad, αB, debemos determinar.
Pero para encontrar esos vectores debemos recurrir a nuestros conocimientos de movimiento circular. |
 |
|
|
|
En particular al movimiento circular uniformemente acelerado, cuyas ecuaciones tienen la siguiente forma:
Θ = Θo + ωo ( t – to ) + ½ γ . ( t – to )²
ω = ωo + γ . ( t – to )
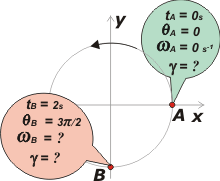
Miremos el segundo esquema que nos va a permitir armar las ecuaciones horarias con seguridad. Tomando como punto inicial al A... |
 |
|
|
|
Nos queda:
Θ = ½ γ . t²
ω = γ . t
Donde γ es la aceleración angular (que no tenés que confundir con ninguna de las anteriores). La aceleración angular describe cómo cambia ω, la velocidad angular. Ya te vas a familiarizar con todas estas magnitudes, no desesperes.
Bueno, teniendo las ecuaciones, pidámosles que hablen del punto B (no te olvides que el ángulo de 270 grados es igual -en radianes- a 3π/2).
3π/2 = ½ γ . 4 s²
ωB = γ . 2 s
Acá hay dos ecuaciones con dos incógnitas, de modo que vamos a poder conocer el valor de ambas. De la primera:
γ = 2,36 s-2
Y eso lo meto en la segunda:
ωB = 4,71 s-1
Luego la aceleración centrípeta y la aceleración tangencial valen:
at = γ . R = 2,36 s-2 . R
acB = ωB2 . R = 22,21 s-2 . R
¡Qué problema! Ambos componentes de la aceleración dependen del radio de giro, que desconocemos. Pero no importa, porque se va a cancelar cuando querramos averiguar el ángulo que estamos buscando, αB. Y finalmente (volvé a mirar el primer esquema) ese ángulo que se forma entre la aceleración y su componente tangencial, αB, valdrá:
αB = arc tg (acB / at) = arc tg (22,21 / 2,36) = arc tg 9,41
Habrás visto que en ese cociente se cancela el valor de del radio, R, no importa cuánto valga. |
|
|
|
|
|
No sé... me parece que no fue tan grave, vos dirás. |
|
|
DESAFIO: ¿Cuánto valdría el ángulo si en lugar de tardar 2 segundos en llegar a B por primera vez hubiera tardado 17,32 segundos? |
|
 |
| Algunos derechos reservados (en criollo: no podés publicarlo a tu nombre, ¿entendiste? Mirá que tengo un boga repesado, ¿eh?).
Eso sí, se permite su reproducción citando la fuente, o sea, a papá. Última actualización dic-19. Buenos Aires, Argentina. |
|
|
| |
|

