 |
NO ME SALEN
EJERCICIOS RESUELTOS DE FÍSICA DEL CBC
(Movimiento Circular Uniforme)
|
|

|
 |
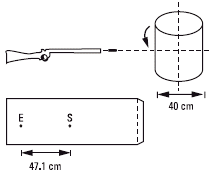
NMS c6.12 - Se hace girar un cilindro hueco de cartulina
alrededor de su eje, a 3.000 rpm. Se dispara
un perdigón de modo que su trayectoria atraviesa
al cilindro, pasando por su eje. |
Al desplegar la
cartulina como muestra el dibujo, puede medirse
la distancia entre orificios.
Hallar la velocidad del proyectil, suponiendo
que el cilindro no dio más de media vuelta mientras
era atravesado. |
 |
|
|
Me encanta este ejercicio: es de esos que no pasan inadvertidos, que no se olvidan. Tiene fama de dificilísimo: muy pocos estudiantes lo abordan, y menos aún lo resuelven. Pero es fácil, creeme; muy fácil. Por eso suelo no resolverlo en clase y, en cambio, doy pistas para tratar de poner en marcha los pensamientos que llevan a plantearlo correctamente.
Acá voy a hacer lo mismo, lo que implica dar demasiadas vueltas... para resolver un problema que se saca con dos reglas de tres simple. Pero podés aprovecharlo para aprender cómo pensar problemas de pura lógica o geometría.
En esta ocasión voy a reproducir los diálogos típicos y las actitudes típicas que se dan con mis estudiantes en clase. Intercalo los gráficos míos -como siempre- e ilustraciones de Roberto Fontanarrosa (a modo de homenaje). |
|
|
| |
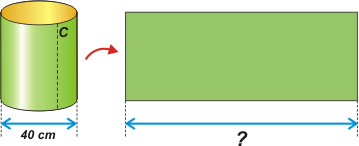
—A ver, mocoso, lo primero es estar seguros de que entendés lo que es un cilindro de cartulina (yo hice un par en la escuela primaria, pero creo que aunque no los hubiese hecho podría imaginarlo correctamente). Si corto por la línea de puntos C el cilindro de 40 cm de diámetro, y despliego la cartulina obtengo un cuadrilátero que tiene un largo de... |
|
|
|
 |
|
|
| |
—Estoy esperando y no tengo todo el tiempo del mundo... Usted lo sabe, mocoso. ¿Deee...?
—No sé... |
|
|
|
 |
Recurso didáctico Nro. 35: cachetazo ascendente de derecha. (M.C.) |
|
|
| |
—¡Ciento veintipico centímetros, maestro!
—Correcto, muchachito. El largo de ese rectángulo es igual a la circunferencia de la base del cilindro. De modo que: pi por diámetro... |
|
|
|
 |
|
|
| |
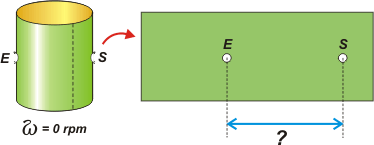
—Ahora que ya sabemos cuánto tiene de largo el cilindro (el alto no interesa para nada), le voy a pedir que imagine que se hace un primer disparo con el rifle, y que perfora al cartón en dos posiciones: entrada, E, y salida, S... pero en una situación en la que el cilindro no está girando. Mire el esquema: |
|
|
|
 |
|
|
| |
—... Y dígame: ¿cuánto están separados los orificios en el cartón desplegado?
—Cuarenta centímetros... |
|
|
|
 |
Recurso didáctico Nro. 71: aplastamiento cefálico con puño derecho (sin fracturas óseas). (M.C.) |
|
|
|
| |
—¿Cómo dijo, mocoso?
—Mmm... nnn... ¡¡¡sesenta y algo!!!
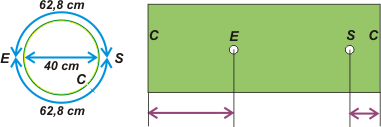
—¡Muy bien, muchacho! Unos 62,8 cm, que son exactamente la mitad de la cartulina. Y dígame -ya que lo veo tan inspirado...- ¿cuánto vale la suma de esos otros dos segmentos que van desde los agujeros hasta los bordes de la cartulina? |
|
|
|
 |
|
|
| |
—62,8 cm también, maestro. Estoy seguro, se lo juro.
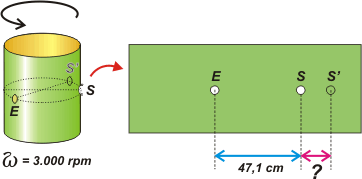
—¡Síííí, muchacho! Porque haga donde haga el corte de la cartulina -habrá visto que en mi esquema lo hice en una posición diferente que la del enunciado del ejercicio- la distancia medida sobre la cartulina a un lado o al otro de las perforaciones, es la misma. Ahora y recién ahora vamos a abordar nuestro problema... en el que la cartulina gira a 3.000 revoluciones por minuto. Mire el esquema, jovencito... venga... levántese... séquese esos mocos. |
|
|
|
 |
|
|
| |
—Preste atención. En este esquemita que representa los orificios de entrada y salida del perdigón en el cilindro girando, y luego desplegado, le representé también la posición del orificio de salida que hubiese hecho si el cilindro no girase, S', o sea, el mismo de antes. ¿Entiende? ¡Abra los ojos, hombre, es sólo un chichón... no se toque!
—Sí, maestro.
—Bueno. Responda: ¿cuánto vale ese segmento que le indiqué en rosa que se corresponde con la distancia entre el orificio de salida, S, y la posición en que estaría hecho el orificio si el cilindro estuviese quieto, S'?
—No sé, maestro. ¡¡¡NOOO!!! ¡¡¡Por favor!!! ¡¡¡Maestroooo...!!! |
|
|
|
 |
| Recurso didáctico Nro. 803: aducir defensa propia. (M.C.) |
|
|
 |
| |
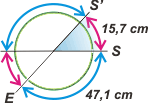
—Se lo voy a decir igual: valía 15,7 cm, que es la diferencia entre los 62,8 de antes y los 47,1 de ahora. Le explico aunque no me escuche: el perdigón perfora la cara delantera del cilindro. Luego -mientras viaja por el interior del cilindro en busca de su cara posterior- el cilindro y su flamante perforación siguen girando; y cuando el perdigón alcanza la cara posterior y realiza la perforación de salida ya han girado un cierto ángulo que al desplegar la cartulina se traduce en una cercanía entre los orificios. ¡Eh...! ¡Oiga! ¡Flojo!... ¡Por un tirito!... |
|
|
| Es una pena... Casi nunca llego a mostrar este último esquemita que aunque es innecesario me permite reforzar esta última imagen: el pedacito de cartón que iba a recibir el impacto por adentro si el cilindro estaba quieto, S', se corrió, le dijo oooleee al perdigón, que salió por otro lugar, S. Y como están parados en la misma calesita: lo que se corrió S' es lo mismo que se movió E. |
|
|
|
Comprendido ésto, lo que resta es una pavada y me daría vergüenza plantear ecuaciones. Lo resuelvo con reglas de tres simple. Acá va la primera: esos 15,7 cm representan un ángulo de (lo voy a hacer en radianes):
62,8 cm → 3,14 rad
15,7 cm → 0,785 rad
Segunda regla de tres. Si en un minuto gira 3.000 veces 6,28 radianes, para girar 0,785 radianes necesita...
18.840 rad → 60 s
0,785 rad → 0,0025 s
Calculo. Si el perdigón va a velocidad constante y tarda 0,0025 s en recorrer el interior del cilindro, su velocidad es:
v = ΔX / Δt = 40 cm/ 0,0025 s
|
|
| |
v = 16.000 cm/s = 160 m/s
|
|
|
|
| DESAFIO: ¿Habría otras respuestas posibles si el enunciado no aclarase "suponiendo
que el cilindro no dio más de media vuelta mientras
era atravesado"? |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente (me refiero a la reproducción de este material didáctico, no a la reproducción sexual de sus lectores, está claro). Última actualización mar-08. Buenos Aires, Argentina. |
|
|
| |
|

