 |
NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA
(Tiro oblicuo)
|
|

|
NMS c5.32* – Un buque navega a 36 km/h en aguas calmas (es decir en reposo respecto de tierra), cuando desde la cubierta de popa se suelta una carga pesada. La carga alcanza el agua luego de 2 segundos.
a) Calcular la altura de la cubierta por encima del agua.
b) Calcular las componentes de la velocidad de la carga al llegar al agua desde un sistema de referencia fijo a tierra y desde un sistema fijo al buque, indicando los respectivos orígenes y sentidos de los ejes.
|
|
| * Este ejercicio formó parte del primer examen parcial de Física del CBC tomado en noviembre de 2012. Para ver el tema de examen completo hacer click acá. |
|
| Este ejercicio es tan sencillo que me da un poco de vergüenza resolverlo formalmente. Pero lo cierto es que resolverlo por la vía rápida no enseña demasiado. La vía expeditiva hay que reservarla, en todo caso, para los exámenes, no para la práctica y el aprendizaje. Arranquemos con un esquema: |
|
|
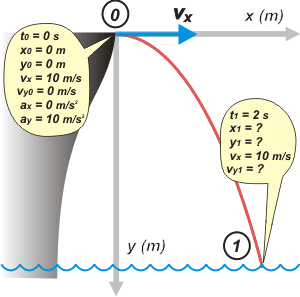 |
Todo esquema te obliga a tomar decisiones: sistema de referencia, nombres de los eventos... e interpretaciones, que en este caso la más importante la velocidad inicial vertical es nula (la carga se suelta), y que la velocidad inicial horizontal es la misma que la del buque.
Ahora vamos a la parte analítica. ¿Cuántas ecuaciones horarias describen este problema? Tres, porsupu, como todo TO. Para hallarlas basta con reemplazar las constantes (to , xo , yo , vx , voy , y g) de las ecuaciones generales de los tiros oblicuos: |
|
|
x = xo + vx ( t – to )
y = yo + voy ( t – to ) + ½ g ( t – to )²
vy = voy + g ( t – to )
En el esquema, en el cuadradito que habla del punto 0, están todas las constantes que necesitamos para armar las ecuaciones que describen el movimiento del cuerpo.
x = 10 m/s . t
y = 5 m/s² . t²
vy = 10 m/s² . t
Ahora les pedimos a esas ecuaciones que hablen del punto 1. |
|
36 km/h =
10 m/s |
 |
x1 = 10 m/s . 2 s |
|
[1] |
| y1 = 5 m/s² . 4 s² |
|
[2] |
| vy1 = 10 m/s² . 2 s |
|
[3] |
|
|
|
Y como siempre... desembocás en un sistema de tantas ecuaciones como incógnitas (en este caso 3 y 3). Resolvelo como quieras. No es física, es álgebra.
La altura de la baranda de la cubierta por encima del agua no es otra cosa que y1. Lo resuelvo de la ecuación [2]. |
|
|
|
|
|
La velocidad vertical de la carga cuando llega al agua nos la cuenta la ecuación [3]:
vy1 = 20 m/s
El resto es sentido común: Visto desde el buque la carga describe de un movimiento vertical. En cambio visto desde la Tierra (o desde el agua quieta) es el tiro oblicuo que resolvimos acá. |
|
|
| |
sistema buque: vx1 = 0 m/s; vy1 = 20 m/s
sistema Tierra: vx1 = 10 m/s; vy1 = 20 m/s |
|
|
|
|
Y con eso estamos. |
|
|
| NOTA: hay una pequeño error en el esquema... pero absolutamente neutral: en lugar de dibujar una popa dibujé una proa. Lo importante es que entiendas que la velocidad inicial del la carga que se suelta es igual a la velocidad del buque... se mueva para donde se mueva. |
|
|
| |
|
|
DESAFIO: ¿Cuánto se desplaza horizontalmente la carga durante su caída? |
|
 |
| Algunos derechos reservados.
O sea: propiedad intelectual, propiedad vertical y propiedad horizontal. Se permite su reproducción citando la fuente. Última actualización jul-14. Buenos Aires, Argentina. |
|
|
| |
|

