 |
NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA
(Tiro oblicuo)

|
|

|
NMS c5.26* - Dos móviles A y B son disparados en el mismo instante y sus vectores velocidad inicial y posición inicial son:
v0A = (10; v0Ay) m/s ; r0A = (0; 0) m ; v0B = (5; 7) m/s ; r0B = (5; 3) m
Determine: el tiempo en que se produce el encuentro, el vector posición en el instante de encuentro y el vector velocidad en el instante de encuentro. |
Cuando leí el ejercicio por primera vez dije lo mismo que vos: chino básico. Pero después comprendí que toda mi impresión negativa pasaba por la notación vectorial con la que nos aportaban los datos. En mi caso fue peor, porque el original tenía errores de notación que lo hacían más ininteligible.
En la versión parcialmente mejorada que te presento igual siguen faltando las flechitas arriba de los vectores y también los versores. pero queda claro que los números (y una incógnita) que están dentro de los paréntesis son las componentes x e y de cada vector.
Empecemos -como siempre- con un esquema... vas a ver como se aclara el panorama. |
|
|
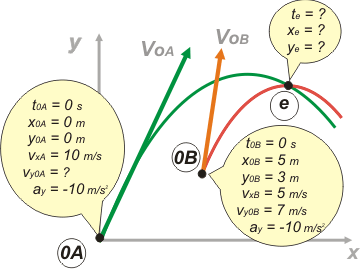 |
No está hecho en escala (no podríamos hasta no conocer las respuestas) pero sí bastante aproximado.
Lo importante es pasar en limpio los datos del ejercicio, poner los nombres que falten y tener a mano las constantes cuando las necesitemos. |
|
|
|
Todo tiro oblicuo se describe con dos ecuaciones de posición (una de posiciones horizontales y otra de alturas) y una de velocidades verticales; tres entonces para cada móvil. Te transcribo los modelos acá: |
|
|
x = xo + vx ( t – to)
y = yo + vo ( t – to) + ½ g ( t – to)²
vy = v0y + ½ g ( t – to)²
|
modelos
(para cualquier TO) |
Para hacer que esos modelos describan el movimiento de cada móvil de este ejercicio en particular, basta con reemplazar las constantes iniciales (to , xo , yo , vx , voy , y g) por las de nuestros movimientos. Algunas no sabemos cuánto valen... pero por lo menos tienen el nombre correcto y ya vamos a averiguar su valor. |
|
| móvil A: |
x = 10 m/s t |
| y = v0Ay t – 5 m/s² . t² |
| vy = v0Ay – 10 m/s² . t² |
|
ecuaciones
(que describen todo el movimiento narrado en el enunciado) |
| móvil B: |
x = 5 m + 5 m/s t |
| y = 3 m + 7 m/s t – 5 m/s² . t² |
| vy = 7 m/s – 10 m/s² . t² |
|
| Ahora les pedimos a las 6 ecuaciones que hablen del instante de encuentro. |
|
| móvil A en el encuentro: |
xe = 10 m/s te |
[1] |
| ye = v0Ay te – 5 m/s² . te² |
[2] |
| veAy = v0Ay – 10 m/s² . te² |
[3] |
|
ecuaciones especializadas
(sólo hablan del momento interesante del ejercicio) |
| móvil B en el encuentro: |
xe = 5 m + 5 m/s te |
[4] |
| ye = 3 m + 7 m/s te – 5 m/s² . te² |
[5] |
| veBy = 7 m/s – 10 m/s² . te² |
[6] |
|
Y a dónde te creés que llegaste: a un sistema de tantas ecuaciones como incógnitas en donde algunas de ellas son las que te pide el enunciado del ejercicio. No inventamos nada, no hicimos para este planteo nada que no hayamos hecho para todos los ejercicios de cinemática... El resto es álgebra. Es muy importante que visualices este límite entre la física y el álgebra. Si lo hacés... ya podés ir sintiéndote físico... porque te lo ganaste.
Por supuesto: hay mil maneras de resolverlo. Yo te muestro una... pero no te olvides que a partir de acá se trata de un ejercicio algebraico. De las ecuaciones [1] y [4] despejamos sale el valor de te.
10 m/s te = 5 m + 5 m/s te
10 m/s te – 5 m/s te = 5 m
5 m/s te = 5 m
|
|
| |
| |
| |
|
|
|
Ahora con ese dato calculo la posición del encuentro en las ecuaciones [1] y [5]
xe = 10 m/s . 1 s = 10 m
ye = 3 m + 7 m/s . 1 s – 5 m/s² . 1 s² = 5 m
Corresponde que respondamos utilizando la misma notación que usa el enunciado. |
|
|
|
|
|
Para calcular las velocidades en el encuentro voy a necesitar la velocidad inicial del móvil A, de modo que en la ecuación [2]...
5 m = v0Ay 1 s – 5 m/s² . 1 s²
v0Ay = 10 m/s`
Ahora con esto voy a la [3]...
veAy = 10 m/s – 10 m/s² . 1 s²
veAy = 0 m/s
Y por otro lado, con la [6]...
veBy= 7 m/s – 10 m/s² . 1 s²
veBy= – 3 m/s
Y como las velocidades de desplazamiento horizontal no cambian durante todo el vuelo, las velocidades en el encuentro serán: |
|
|
| |
veA = (10; 0) m/s ; veB = (5; –3) m/s |
|
|
|
|
| |
|
|
Comentario: Esta notación vectorial se llama par ordenado. En la literatura anglosajona las componentes se separan con comas y en la literatura latina con punto y coma. |
|
|
| Desafíos: Ahora sí, podés hacer un esquema a escala, vas a ver que es bastante diferente del que usé acá. |
|
 |
| |
|
| *Este ejercicio (modificado) fue tomado de la guía de ejercicios de la Universidad Tecnológica Nacional (UTN), Regional Buenos Aires. Algunos derechos reservados (en criollo: no podés publicarlo a tu nombre, ¿entendiste? Mirá que tengo un boga repesado, ¿eh?).
Eso sí, se permite su reproducción citando la fuente. Última actualización ene-13. Buenos Aires, Argentina. |
|
|
|

