 |
NO ME SALEN
EJERCICIOS RESUELTOS DE FÍSICA
(Movimientos variados)
|
|

|
NMS c5.20- Un cañón de un barco lanza horizontalmente, desde una altura de 5 metros respecto al nivel del mar, un proyectil con una velocidad inicial de 900 m/s. Si el tubo del cañón es de 15 m de longitud y se supone que el movimiento del proyectil dentro del tubo es uniformemente acelerado, debido a la fuerza constante de los gases de la combustión de la pólvora, calcular:
a) La aceleración del proyectil dentro del cañón y el tiempo invertido por el proyectil en recorrer el tubo del cañón.
b) La distancia horizontal alcanzada por el proyectil desde que abandona el cañón hasta que se introduce en el agua.
|
|
No me canso de decirlo: los enunciados siempre hay que leerlos un par de veces o más, hasta que uno no se haya hecho una idea cabal de lo que ocurre. Y después hay que leerlo una vez más para chequear que lo que uno haya entendido sea, efectivamente, lo que el enunciado plantea.
En este ejercicio tenés dos movimientos independientes, que tenés que plantear por separado: un MRUV dentro del cañón y un TO en el aire. Empecemos con el cañón. |
Como siempre hacemos un esquema con el que le pongo nombre a los eventos que voy a utilizar; y en forma automática quedan bautizadas todas las constantes y variables, ya sean datos o incógnitas.
Como todo MRUV, se describe con 2 ecuaciones: |
 |
|
|
|
x = ½ a t2
v = a t
Si a esas dos ecuaciones les pido que hablen del punto S, ellas dirán:
15 m = ½ a tS2
900 m/s = a tS
Si lo mirás con cariño, tenés ahí dos ecuaciones con dos incógnitas... de modo que eso tiene solución algebraica... y la encontrás (de la segunda despejá una de las incógnitas, y lo que te dé ese despeje lo metés en la primera): |
|
| para armar las ecuaciones utilicé las constantes del punto A |
|
| |
tS = 0,033 s, a = 27.000 m/s2 |
|
|
|
|
Ahora vamos al TO en el aire marino. |
|
|
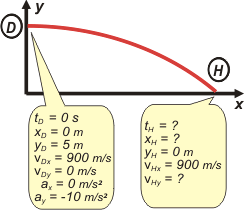
Como siempre hacemos un esquema con el que le pongo nombre a los eventos que voy a utilizar; y en forma automática quedan bautizadas todas las constantes y variables, ya sean datos o incógnitas.
Fijate que llamé D (por disparo) a lo mismo que en la parte anterior llamé S (por salida). Se trata del mismo evento: la salida de la bala por la boca del cañón. Le puse distinto nombre, porque cambié la escala de tiempo para que tus ecuaciones sean más sencillas. (No debería hacerlo, pero me gusta caminar por la calle sin tener que llevar casco).
Como todo TO, se describe con 3 ecuaciones: |
 |
|
|
|
x = 900 m/s . t
y = 5 m – 5 m/s2 . t2
vy = – 10 m/s2 . t
|
|
| para armar las ecuaciones utilicé las constantes del punto D |
|
A las 3 ecuaciones les pedimos que hablen de punto H (donde la bala se hunde).
xH = 900 m/s . tH
0 m = 5 m – 5 m/s2 . tH2
vHy = – 10 m/s2 . tH
|
|
|
Y si lo mirás bien, tenés 3 ecuaciones con 3 incógnitas, una de las cuales es la que te solicita el enunciado. El resto es álgebra: despejá de la segunda tH, calculalo, y reemplazá ese valor en la primera. |
|
|
|
|
|
Como ves... era una papa. |
|
|
DESAFIO: ¿con qué velocidad se zambulle la bala en el mar? ¿Cuánto más lejos llegaría la bala si al cañón se le da una elevación de 15 grados? |
|
 |
| Algunos derechos reservados. El lugar más seguro para viajar en tren es ir en micro. Última actualización oct-11. Buenos Aires, Argentina. |
|
|
| |
|

