 |
NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Tiro oblicuo)

|
|

|
NMS c5.16* - Un globo asciende verticalmente a 2 m/s. Cuando se encuentra a una altura de 18 m un pasajero del globo arroja un hueso a 4 m/s y horizontalmente (respecto a él). Simultáneamente un perro sale corriendo y lo atrapa justo antes de que toque el piso. Suponiendo que el perro se mueve a aceleración constante, ¿cuál es el valor de esa aceleración?
Como siempre empecemos con un esquema: acá se ve, con más fuerza que nunca, cuán potente es esta herramienta. |
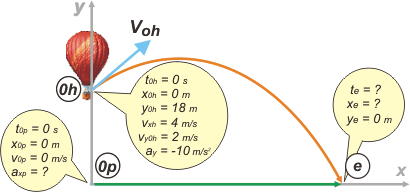 |
La mayoría de los estudiantes yerran en este ejercicio porque olvidan la componente vertical de la velocidad inicial. El pasajero arroja el hueso en forma horizontal... pero el globo, y él, y su mano, y su hueso ya están animados con una velocidad de ascenso. |
|
Se trata de un encuentro entre un móvil que viaja en un tiro oblicuo (el hueso) y otro que se mueve rectilíneamente en forma acelerada (el perro). Entonces, si tenés los modelos de ecuación horaria a la vista... |
|
|
TO (X) → x = xoh + vxh ( t – toh)
TO (Y) → y = yoh + vohy ( t – toh) + ½ g ( t – toh)²
MRUV → x = xop + vop ( t – top) + ½ ap ( t – top)²
|
modelos
(para cualquier TO, y para cualquier MRUV) |
| ... podemos empezar. Lo primero que hacemos es armar las ecuaciones horarias de nuestros móviles, reemplazando las constantes (top, toh, xop, xoh, yoh, vxh, vohy, vop, ap y g) que figuran en los globitos de los instantes iniciales. (Te habrás dado cuenta de que usé h por hueso, y p por perro... no yo, el perro del ejercicio). |
|
hueso → x = 4 m/s . t
hueso → y = 18 m + 2 m/s . t – 5 m/s² . t²
perro → x = ½ ap . t ²
|
ecuaciones
(para todo el el movimiento del ejercicio) |
| Ahora les pedimos a las tres ecuaciones que hablen del punto del encuentro feliz. |
|
xe = 4 m/s . te
0 m = 18 m + 2 m/s . te – 5 m/s² . te²
xe = ½ ap . te ²
|
ecuaciones especializadas
(sólo hablan del momento del encuentro) |
Se trata de un sistema bastante sencillo. Te cuento cuál es el plan: con la segunda ecuación vamos a averiguar cuánto vale el instante de encuentro (fijate que es una ecuación cuadrática que por suerte ya está igualada a cero, y que va a arrojar dos valores de te, de los cuales descartaremos uno por inapropiado); con ese valor vamos a la primera ecuación y averiguamos la posición de encuentro; finalmente, en la tercera, sale la aceleración del perrito. Vamos. |
|
a = – 5 m/s² , b = 2 m/s y c = 18 m
|
|
|
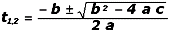
|
|
|
te = 2,1 s
xe = 4 m/s . 2,1 s = 8,4 m
ap= 2 . xe / te ² = 2 . 8,4 m / 4,4 s²
|
|
|
|
|
|
| * Este ejercicio fue tomado en el 1er. examen parcial de Ciudad Universitaria, en mayo de 2008. |
|
|
| |
|
|
| DESAFIO: ¿Cuál tendría que haber sido la posición inicial del perro si sólo pudiese acelerar a 2 m/s²? |
|
 |
| |
|
| Algunos derechos reservados (en criollo: no podés publicarlo a tu nombre, ¿entendiste? Mirá que tengo un boga repesado, ¿eh?).
Eso sí, se permite su reproducción citando la fuente. Última actualización may-08. Buenos Aires, Argentina. |
|
|
|

