NO ME SALEN
SOLVED PHYSICS EXCERCISES FROM THE CBC
|
|

|
Aditional No me salen 5.14* - A cargo train is moving with a constant speed of 30 km/h. A man in one of the the wagons, throws a ball to the air and picks it up when it falls. Respecting to the wagon, the ball´s initial speed is 45 km/h vertically, upwards.
|
a) Wich are the modulus and the direction of the ball´s initial speed, seen by another man, standing alongisde the tracks?
b) For how long does the ball stay in the air according to every one of the observers?
c) How much horizontal distance does the ball travels while it is in the air according to each one of the observers?
d) Wich is the ball´s minimum speed according to each one of the observers?
e) Wich is the acceleration of the ball according to each one of the observers? |
|
|
|
This is a trully beautifull excercise, it is so simple and yet so instructive, for that, this excercise should be written in every book of physics in existence. It shows wonderfully the problem that Galileo Galilei had to put up with when he started his journey against the aristotelic conception of the world, and it shows the deep existing relation between relative movement and oblique shot. It is one of the most pretty roses that Galileo left us, from his main rosebush.
Allow me to do this reflexion first: pretend for a moment that you are a witness of these facts and that you are inside the wagon, with the ballthrower. Suppose, besides that, that the wagon does not have any windows to the outside, and that, it is so, so modern, that when it moves, you can not feel it. Are you capable of imagining all of those things? |
|
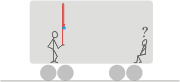 |
Well, you are the one sitting, and there you wander what can you do, while the ballthrower plays with his ball. Have some patience, you are going to do something very important.
To begin with, tell me if, by looking the ball, you can deduce if the train is moving or not. |
|
|
If you´ve meditated long enough, you would have found that the question has no answer. It can not be deduced just by looking at the ball. The ballthrower tosses it vertically and receives it in the same place where the launching took place. That will occur wether the wagon is moving with constant speed or if it is not moving at all. Let´s call the outside observer. |
|
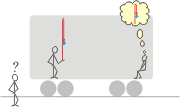 |
There he is. Now it is he who is asking why we called him. He has no problem at all (let´s hope that for his health) to nottice if the wagon is moving or not. In the hypothetical scenario where the wagon is not moving (and the wagon´s walls were transparent) he would see the same as you: a common and friendly vertical shot. |
|
|
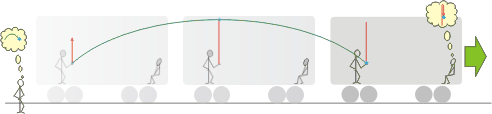
| But, what would he see if the wagon was moving? In that case, your perception of the shot and the perception from the other guy would be different... He would see the ball as a oblique shot! |
|
 |
|
| Now it seems obvious, but for Galileo it was one of the most hard headaches ever. He needed that the trayectory seen from outside the wagon was an oblique shot. He needed that the trayectory was the result from the composition of two movements: one horizontal from the uniform translation, and one vertical, simple and free. That was the only way to admit that the Earth didn´t have to stay put. |
|
 |
How could an oblique shot be the result from a perfectly vertical shot, like the one that the ballthrower is doing? The answer is that the ballthrower, and his hand, and his feet, and the wagon -and also you- are moving forward with speed, that the thrower transfers to the ball (in an involuntary way). That speed is not lost: it stays constant, being that during the time the ball is in the air, there is nothing stopping it. |
|
|
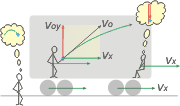
The ball´s speed (seen by the outside observer) is: v = vx + vy (vectorial relation), where vy is the ball´s speed according to you, and vx is the ball´s lateral displacement, and also your speed, along with the train, as seen by the outside observer.
This way, the brilliant decomposition of the oblique shot movement into two independent movements, melts with the relative movement equation and tells us that the kinematic phenomenons have exactly the same aspect for the passengers of the train -or for the fully earthlings-, whether the train –or the Earth. is moving or not.
Well, I got sidetracked. I was a little excited. Let´s answer the questions.
a) Wich are the the modulus and the initial speed´s direction of the ball, according to another man standing alongside de tracks? As you can see in the last drawing, the initial speed, observed from the outside, is the vectorial composition between the vertical, caused by the the ballthrower, and the horizontal, caused by the movement inflicted on his hand by the wagon´s speed. It comes up easy, using Pitágoras. The answer is 54,1 km/h orl, 15 m/s; and it forms and angle of 56,3 degrees.
b ) For how long does the ball stay in the air according to every one of the observers? It´s the same for everybody (pretty obvious, right?... Well, not so obvious for Einstein). To know how long, use the vertical time equation for oblique shots (the same you are seeing there, sitting in the wagon)
y = 12,5 m/s – 5 m/s² . t ²
(I changed the units to meters and seconds). I ask that equation to tell me about the cero height, that means, when it returns to my hand, and she tells me 2,5 s.
c) How much horizontal distance does the ball travels while it is in the air according to each one of the observers? With this data, I go to the ball´s horizontal kinetic equation
x = 8,3 m/s . t
And I ask her to tell me where is the ball in the instant 2,5 s. She answers gently: 20,83 m.
d) Wich is the ball´s minimum speed according to each one of the observers?
For the observer inside the wagon (that means, you), is cero, and it matches with the highest point the ball reaches, right?. But for the observer outside the wagon, it is 8,33 m/s and that happens in the same instant the ball reaches the shot´s highest point.
e) Wich is the acceleration of the ball according to each one of the observers? It´s the same for everyone: it only affects the movement in the vertical direction, and it´s approximately 10 m/s². |
|
| CHALLENGE 1: Galileo carried out the investigations about the trajectory of proyectiles with a really brilliant artifact wich allowed him to register trajectories and observe them in ``slow-mo´´. I bet you that you search it and you find it. CHALLENGE 2: here I write the speed equation according to the dude watching from outside of the wagon, and according to Galileo´s equation, that is, the relative movement equation: v = vx + vy. Transform it in a temporal equation. Do you dare? |
|
| |
 |
| |
*Excercise extracted from the CBC Guide of physics problems, used until the year 2003. It´s about the aditional 7.1 (page 99). |
|
| |
|
Some Rights Reserved. Not allowed to be copied without naming either the author or this source material. Those ones not obeying these rules will be sentenced to hard labor in the Antarctica. Translated by Santi Pisci. Last updated ago-15. Buenos Aires, Argentina. |
|
|

